LN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 8 2023
Tham khảo
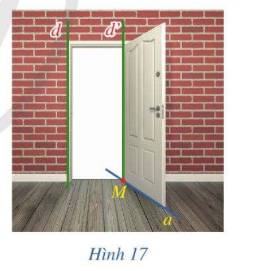
Vì sàn nhà là một mặt phẳng vuông góc với đường thẳng d. Mà đường thẳng a luôn nằm trên mặt phẳng đó nên đường thẳng d luôn vuông góc với đường thẳng a
13 tháng 8 2023
a: \(a\perp\left(Q\right);\Delta\subset\left(Q\right)\)
=>\(\Delta\perp a\)(1)
\(b\perp\left(R\right);\Delta\subset\left(R\right)\)
=>\(\Delta\perp b\)(2)
mà a,b thuộc (P)(3)
nên từ (1), (2), (3) suy ra \(\Delta\perp\left(P\right)\)
b: Có 1 đường duy nhất
23 tháng 8 2023
Do mặt bàn và mặt đất không có điểm chung nên chúng song song với nhau.
QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
M thuộc c suy ra M nằm trên mp(Q)
M thuộc a suy ra M nằm trên mp(R)
M cùng thuộc mp(R) và (Q) suy ra M nằm trên giao tuyến của mp(R) và (Q)
Như vậy , M thuộc b.
16 tháng 8 2023
tham khảo:
Trong một phòng, mặt sàn và các mặt tường đều vuông góc với nhau. Khi cánh cửa được đóng lại, thì mặt cửa cũng vuông góc với cả mặt sàn và mặt tường, nên đường thẳng nối bán lề của cánh cửa và cạnh của phòng sẽ là đường thẳng vuông góc với sàn nhà.
Trong quá trình đóng - mở cánh cửa, bán lề của cánh cửa vẫn cố định với mặt tường, nên đường thẳng nối bán lề của cánh cửa và cạnh của phòng vẫn là đường thẳng vuông góc với sàn nhà. Từ đó suy ra, trong quá trình đóng - mở, cánh cửa luôn vuông góc với sàn nhà.
QT
Quoc Tran Anh Le
Giáo viên
25 tháng 8 2023
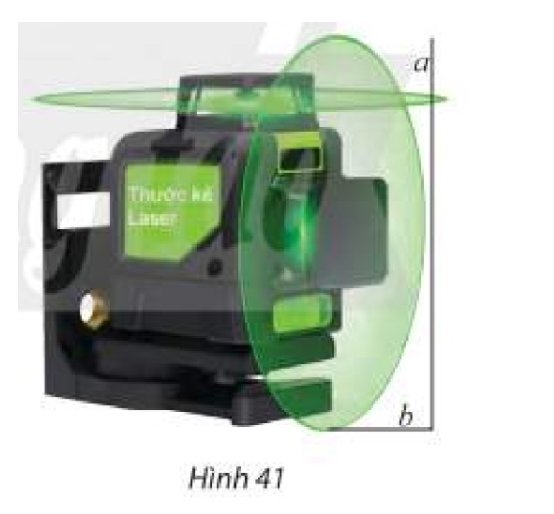
Do tia laser quay sẽ tạo ra một mặt phẳng, mặt phẳng này giao với mặt phẳng tường hoặc sàn nhà tạo thành một đường thẳng. Do đó có thể giúp người thợ kẻ được đường thẳng trên tường hoặc sàn nhà.
CM
6 tháng 12 2017
a) Sai
Sửa lại: "Đường thẳng Δ là đường thẳng vuông góc chung của hai đường thẳng chéo nhau a và b nếu Δ cắt cả a và b, đồng thời Δ ⊥ a và Δ ⊥ b"
b) Đúng
c) Đúng
d) Sai
Sửa lại: Đường thẳng đi qua M trên a và vuông góc với a, đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.
e) Sai.
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
a) Vì (P) // (Q), (R) cắt (P) suy ra (R) cũng cắt (Q).
b) a và b lần lượt là giao tuyến của (R) và các mp(P), (Q) do đó a và b đồng phẳng suy ra a và b không thể chéo nhau.
Mà a và b lần lượt thuộc hai mặt phẳng song song (P) và (Q) suy ra a // b.
CM
27 tháng 9 2018
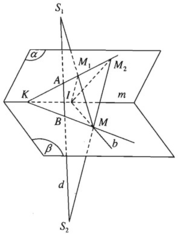
a) Mặt phẳng (M, d) cắt (α) theo giao tuyến M 1 M 2 . Điểm A cũng thuộc giao tuyến đó. Vậy đường thẳng M 1 M 2 luôn luôn đi qua điểm A cố định.
b) Mặt phẳng (M, d) cắt (β) theo giao tuyến BM. Điểm K thuộc giao tuyến đó nên ba điểm K, B, M thẳng hàng.
c) Giả sử b cắt m tại I thì mặt phẳng ( S 1 , b ) luôn luôn cắt (α) theo giao tuyến I M 1 . Do đó điểm M 1 di động trên giao tuyến của I M 1 cố định. Còn khi M di động trên b thì mặt phẳng ( S 2 , b ) cắt (α) theo giao tuyến I M 2 . Do đó điểm M 2 chạy trên giao tuyến I M 2 cố định.