hãy chứng minh rằng 1=2

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

NV

Nguyễn Việt An

19 tháng 2 2021 - olm

hãy chứng minh rằng 1=2

#Hỏi cộng đồng OLM #Toán lớp 7

2

LN

Lê Nguyễn Gia Vy

19 tháng 2 2021

1 đôi dày = 2 chiếc dày

LN

Lê Nguyễn Gia Vy

19 tháng 2 2021

1 đôi dày = 2 chiếc dày

Các câu hỏi dưới đây có thể giống với câu hỏi trên

PT

Pham Trong Bach

12 tháng 6 2017

Biết rằng: b z - c y a = c x - a z b = a y - b x c ...

#Hỏi cộng đồng OLM #Toán lớp 7

1

CM

Cao Minh Tâm

12 tháng 6 2017

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

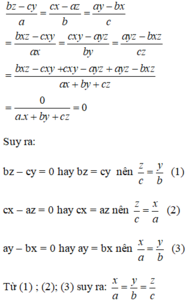
Giải sách bài tập Toán 7 | Giải sbt Toán 7

Hay x : y : z = a : b : c

VR

VRCT_Vip royal character titanic

26 tháng 5 2016 - olm

Câu hỏi nhóm BGS số 5 - lớp 7

1.Chứng minh rằng phương trình x²+2x+2 không có nghiệm.

2.Chứng minh rằng phương trình x²+x+1 không có nghiệm.

#Hỏi cộng đồng OLM #Toán lớp 7

1

HL

Hoàng Lê Bảo Ngọc

26 tháng 5 2016

1. \(x^2+2x+2=x^2+2x+1+1=\left(x+1\right)^2+1\ge1>0\)

=> Dấu đẳng thức không xảy ra => Phương trình vô nghiệm.

2. \(x^2+x+1=x^2+\frac{2.x.1}{2}+\frac{1}{4}-\frac{1}{4}+1=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\)

=> Dấu đẳng thức không xảy ra = > Phương trình vô nghiệm.

Cách giải thích khác : Vì \(x^2+x+1\)là bình phương thiếu của một tổng nên vô nghiệm.

Xin chào nhóm của bạn!

S

Shinnôsuke

31 tháng 3 2016 - olm

Hãy chứng tỏ rằng

A=0,5(2007^2005-2003^2003) là một số nguyên

#Hỏi cộng đồng OLM #Toán lớp 7

0

NV

nguyen van duy

30 tháng 11 2014 - olm

cho tam giác ABC có các điểm D, E theo thứ tự là trung điểm của AB, AC. trên tia DE lấy điểm F sao cho DE = EF

a) chứng minh rằng: tam giác AED = tam giác CEF và có nhận xét ji về DÂE và FCÊ

b) chứng minh rằng: AD // CF

c) Đường thẳng qua E và song song với AB cắt BC ở F. chứng minh rằng DE = 1 /2 BC

#Hỏi cộng đồng OLM #Toán lớp 7

0

HN

Hà Ngọc Uyên Phương

10 tháng 2 2022 - olm

Bài 1: Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.a) Chứng minh rằng :HB=HCb) Chứng minh rằng: AH là tia phân giác của góc ABài 2: Cho tam giác ABC cân tại A có góc A < 90 độ. Vẽ BM vuông góc với AC tại M, CN vuông góc với AB tại Na) Chứng minh AM= ANb) Gọi I là giao điểm của BM và CN. Chứng minh rằng AI là tia phân giác của góc...

#Hỏi cộng đồng OLM #Toán lớp 7

1

DH

Dương Hoàng Bách

10 tháng 2 2022

b1

a) CM tam giác chứaHB và chứa HC = nhau

b) CM tam giác chứa 2 góc A = nhau

NH

Nguyen Hai Bang

25 tháng 7 2016 - olm

Câu hỏi hay

1. Chứng minh rằng \(\frac{8.10^{2016}+2017}{9}\)là 1 số tự nhiên

2. Chứng minh rằng A= \(220^{11969}\)+ \(119^{69220}\)+ \(69^{220119}\) chia hết cho 102

#Hỏi cộng đồng OLM #Toán lớp 7

1

NT

Nguyễn Thiên Kim

25 tháng 7 2016

\(1.\)Ta có: \(8.10^{2016}+2017=8.10...000+2017=80...000+2017=80...2017\)

Mà tổng các chữ số của số trên là: \(8+0+...+2+0+1+7=18\)chia hết cho 9

\(\Rightarrow\)\(8.10^{2016}+2017\)chia hết cho 9

Vậy \(\frac{8.10^{2016}+2017}{9}\)có giá trị là 1 số tự nhiên.

\(2.\)Ta có: 220 đồng dư với 0 (mod 2) nên \(220^{11969}\)đồng dư với 0 (mod 2)

119 đồng dư với 1 (mod 2) nên \(119^{69220}\)đồng dư với 1 (mod 2)

69 đồng dư với -1 (mod 2) nên \(69^{220119}\)đồng dư với -1 (mod 2)

Vậy A đồng dư với 0 (mod 2) suy ra A chia hết cho 2.

Mặt khác: 220 đồng dư với 1 (mod 3) nên \(220^{11969}\)đồng dư với 1 (mod 3)

119 đồng dư với -1 (mod 3) nên \(119^{69220}\)đồng dư với -1 (mod 3)

69 đồng dư với 0 (mod 3) nên \(69^{220119}\)đồng dư với 0 (mod 3)

Vậy A đồng dư với 0 (mod 3) suy ra A chia hết cho 3.

Ta lại có: 220 đồng dư với -1 (mod 17) nên \(220^{11969}\)đồng dư với -1 (mod 17)

119 đồng dư với 0 (mod 17) nên \(119^{69220}\)đồng dư với 0 (mod 17)

69 đồng dư với 1 (mod 17) nên \(69^{220119}\)đồng dư với 1 (mod 17)

Vậy A đồng dư với 0 (mod 17) suy ra A chia hết cho 17.

Vì 2, 3, 17 là các số nguyên tố \(\Rightarrow\)A chia hết cho 102 (vì 2.3.17 = 102).

KS

Kudo Shinichi

3 tháng 3 2019 - olm

Cho 1/c=1/2(1/a+1/b).Chứng minh rằng a/b=(a-c)/(c-b)

#Hỏi cộng đồng OLM #Toán lớp 7

1

NL

Nguyễn Linh Chi

1 tháng 1 2020

Câu hỏi của nguyen thanh chuc - Toán lớp 7 - Học toán với OnlineMath

LN

Linh nguyen thuy

25 tháng 3 2020

Cho tam giasc ABC có AB= 1cm, AC= 6cm

a. Hãy tìm độ dài cạnh BC, biết độ dài cạnh này là 1 số nguyên lẻ

b. Lấy điểm D nằm bên trong tam giác. Chứng minh rằng MA+ MB+ MC> 8

#Hỏi cộng đồng OLM #Toán lớp 7

0

L

lethuydung

14 tháng 12 2016 - olm

Chứng minh rằng :

A = 2011/2010^2+1 + 2011/2010^2+2 + ... + 2011/2010^2 +2010

#Hỏi cộng đồng OLM #Toán lớp 7

0

VT

Vũ Trang

6 tháng 3 2017

Chứng minh rằng: Nếu (a;b) = 1 thì (a²; a + b) =1

#Hỏi cộng đồng OLM #Toán lớp 7

1

HH

Hoang Hung Quan

6 tháng 3 2017

Giải:

Gọi \(ƯCLN\left(a^2;a+b\right)=1\)

\(\Rightarrow\left\{\begin{matrix}a^2⋮d\\a+b⋮d\end{matrix}\right.\Rightarrow\left\{\begin{matrix}a\left(a+b\right)⋮d\\a^2+ab⋮d\end{matrix}\right.\)

\(\Rightarrow a^2+ab-a^2⋮d\)

\(\Rightarrow ab⋮d\)

Mà \(\left(a;b\right)=1\Rightarrow\left\{\begin{matrix}a⋮d\\b⋮d\end{matrix}\right.\)

Nếu \(a⋮d\)

\(\Rightarrow a+b⋮d\Rightarrow b⋮d\)

\(\Rightarrow d\inƯC\left(a;b\right)\)

Mà \(ƯCLN\left(a;b\right)=1\Rightarrow d=1\RightarrowƯCLN\left(a^2;a+b\right)=1\)

Nếu \(b⋮d\)

\(\Rightarrow a+b⋮d\Rightarrow a⋮d\)

\(\Rightarrow d\inƯC\left(a;b\right)\)

Mà \(ƯCLN\left(a;b\right)=1\Rightarrow d=1\RightarrowƯCLN\left(a^2;a+b\right)=1\)

Vậy nếu \(\left(a;b\right)=1\) thì \(\left(a^2;a+b\right)=1\) (Đpcm)