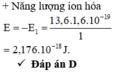Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Công thức (1) và (2) đều đúng em nhé. Nhưng em nói I và cosφ là một nên có chung công thức là không đúng trong trường hợp này.
Vì trong trường hợp (1) có suất điện động E thay đổi theo n.
I = E/Z, trong trường hợp này E thay đổi theo tốc độ quay n bạn nhé.

Bạn áp dụng kết quả này của mạch RLC khi $w$ thay đổi để $U_C$max nhé:
\(\tan\varphi_{RL}.\tan\varphi_{mạch}=0,5\)
\(\tan\varphi_{RL}=\frac{Z_L}{R}=\frac{U_L}{U_R}=0,1\)
\(\Rightarrow\tan\varphi_{mạch}=5\)
\(\Rightarrow\cos\varphi=\frac{1}{\sqrt{1+\tan^2\varphi}}=\frac{1}{\sqrt{26}}\)

Áp dụng kết quả chuẩn hóa của bài toán ω thay đổi để điện áp hiệu dụng trên tụ điện cực đại, khi đó Z L = 1 Z C = n R = 2 n − 2
→ U L = 0 , 1 U R ⇔ Z L = 0 , 1 R ⇔ 1 = 0 , 1 2 n − 2
→ n = 51
Hệ số công suất của mạch khi đó
cos φ = 2 1 + n = 2 1 + 51 = 1 26
Đáp án D

Tần số thay đổi để Uc max thì: \(\omega=\frac{1}{L}\sqrt{\frac{L}{C}-\frac{R^2}{2}}=\frac{\pi}{2}\sqrt{\frac{2.\pi}{\pi.4.10^{-4}}-\frac{2.30^2}{2}}=5\sqrt{41}\pi\)
Công suất tiêu thụ: \(P=\frac{U^2}{R^2+\left(Z_L-Z_C\right)^2}.R=\frac{2.100^2}{2.30^2+\left(5\sqrt{41}\pi\frac{2}{\pi}-\frac{1}{5\sqrt{41}\pi.\frac{4.10^{-4}}{\pi}}\right)^2}.30\sqrt{2}\)\(=530W\)

\(I_1 = I_2\)
<=> \(\frac{U_1}{\sqrt{R^2 + (Z_{L1}-Z_{C1})^2}} = \frac{U_2}{\sqrt{R^2 + (Z_{L2}-Z_{C2})^2}}\)
<=> \((Z_{L1} -Z_{C1})^2 = (Z_{L2} -Z_{C2})^2 \) (do \(U_1 = U_2=U= const\))
<=> \(\omega_1L - \frac{1}{\omega_1C} = \omega_2L - \frac{1}{\omega_2C} => \omega_1 = \omega_2\) (loại)
hoặc \(\omega_1L - \frac{1}{\omega_1C} =- \omega_2L + \frac{1}{\omega_2C}\)=> \(L(\omega_1+ \omega_2) = \frac{1}{C} \frac{\omega_1+\omega_2}{\omega_1\omega_2}\)
=> \(\omega_1\omega_2 = \frac{1}{LC}.\)
Chọn đáp án.A.\(\omega_1\omega_2 = \frac{1}{LC}\)