Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
Có thể vẽ hình như sau:
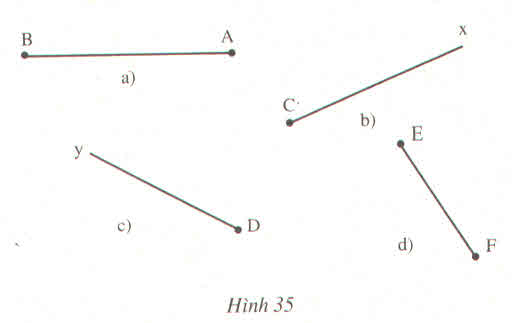
a) Đỉnh của góc là A, một cạnh là AB, cần vẽ tia AC.
b) Đỉnh của góc là C, một cạnh là Cx, cần vẽ tia Cz.
c) Đỉnh của góc là D, một cạnh là Dy, cần vẽ tia Dx.
d) Đỉnh của góc là F, Một cạnh là EF, cần vẽ tia Fy.

vi tia AM va AN doi nhau
=>MAP va PAN la goc ke bu
=>MAP+PAN=180'.Ma PAM=33' nen ta co 33'+PAN=180'
=>PAN=180'-33'=147'
vi tia AQ nam giua 2 tia APva AN
=>PAQ+QAN=147'
=>PAN=147'-QAN=147'-58'=89'

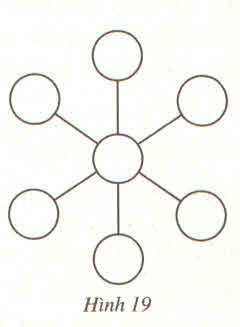
Trước hết ta cần nhận xét:
\(\left(-1\right)+\left(-2\right)+\left(-3\right)+\left(-4\right)+5+6+7=8\)
Mặt khác, tổng của ba bộ số "thẳng hàng" bằng 0 nên ta có tổng của sáu số xung quanh và ba số đứng giũa cũng bằng 0.
Từ đó suy ra: Số đứng giữa + số đứng giữa +8 = 0, nên số đứng giữa = -4.
Từ đó, ta có cách điền như hình 19 dưới đây
-4 -3 -2 -1 7 6 5 Hình 19
Trước hết ta cần nhận xét:
\(\left(1\right)+\left(-2\right)+-3+\left(-4\right)+5+6+7=8\)
Mặt khác, tổng của ba bộ số "thẳng hàng" bằng 0 nên ta có tổng của sáu số xung quanh và ba số đứng giũa cũng bằng 0.
Từ đó suy ra: Số đứng giữa + số đứng giữa +8 = 0, nên số đứng giữa = -4.
Từ đó, ta có cách điền như hình 19 dưới đây
7 6 5 -4 -3 -2 -1 Hình 19

Ta có : \(\dfrac{1}{2}xOy=\dfrac{1}{7}yOz\Rightarrow xOy=\dfrac{1}{7}yOz:\dfrac{1}{2}=\dfrac{2}{7}yOz\)
Ta lại có : góc xOy + góc yOz = 180 độ( hai góc kề bù )
\(\Rightarrow\) \(\dfrac{2}{7}yOz\) + góc yOz = 180 độ
\(\Rightarrow\)yOz(\(\dfrac{2}{7}+1\)) = 180 độ
\(\Rightarrow\)\(\dfrac{9}{7}yOz\)= 180 độ
\(\Rightarrow\)yOz = 180 : \(\dfrac{9}{7}\)=180 .\(\dfrac{7}{9}\)= 140 độ
Khi đó : xOy = 140 . \(\dfrac{2}{7}\)= 40 độ

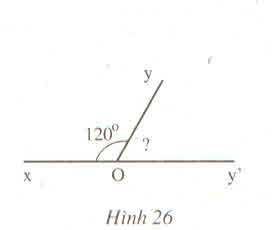
ta có : xOy va yOy' la hai goc ke nhau
=) xOy = 180 do
=> yOy' + xOy = xOy'
=> yOy' = xOy' - xOy =180 - 120 = 60 do
vay yOy' = 60 do

3/ Chu vi hình chữ nhật:
\(\left(\dfrac{1}{4}+\dfrac{3}{10}\right)\cdot2=\dfrac{11}{10}\) (chưa biết đơn vị)
Diện tích hình chữ nhật:
\(\dfrac{1}{4}\cdot\dfrac{3}{10}=\dfrac{11}{20}\) (chưa biết đơn vị)
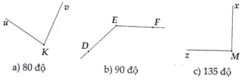


a ) u K v ^ = 80 ° . b ) D E F ^ = 135 ° . c ) z M x ^ = 90 °