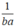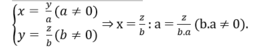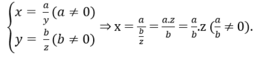Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi số tiền của ba người lần lượt là a (đồng), b (đồng), c (đồng)
+ Vì số tiền của từng người tỉ lệ với 2, 3, 4 nên:
a/2 = b/3 = c/4
+ Vì tổng số tiền của cả 3 người là 75000 đồng nên:
a + b + c = 75000
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
a/2 = b/3 = c/4 = a + b + c / 2 + 3 + 4 = 75000/9 = 8333, (3)
a/2 = 8333, (3) => a = 8333, (3) . 2 = 16666, (6) \(\approx\) 17000
b/3 = 8333, (3) => b = 8333, (3) . 3 = 25000
c/4 = 8333, (3) => c = 8333, (3) . 4 = 33333, (3) \(\approx\) 33000
Vậy số tiền của từng người là 17000 đồng, 25000 đồng và 33000 đồng.
Gọi 3 phần lần lượt tìm là a,b,c :
5a = 2b , 3b = 7c biết rằng a + b + c = 640
\(\Leftrightarrow\frac{a}{2}=\frac{b}{5};\frac{b}{7}=\frac{c}{3}\)
\(\Leftrightarrow\frac{a}{14}=\frac{b}{35}=\frac{c}{15}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có :
\(\frac{a}{b}=\frac{b}{35}=\frac{c}{15}=\frac{a+b+c}{14+35+15}=\frac{640}{64}=10\)
\(\Leftrightarrow\frac{a}{14}=10;\frac{b}{35}=10;\frac{c}{15}=10\)
\(\Leftrightarrow a=140;b=350;c=150\)
mình làm trước k nhe
gọi x, y, z là ba phần của số 520
Theo đề bài, ta có:
x+y+z=520; \(\frac{X}{\frac{1}{2}}=\frac{y}{\frac{1}{3}}=\frac{z}{\frac{1}{4}}\)
Giải theo kiểu tỉ lệ nghịch là nó ra.
Gọi 3 số cần tìm là a;b và c.
Ta có số thứ nhất và số thứ hai tỉ lệ nghịch với 5 và 2.
=> a và b tỉ lệ thuận với\(\frac{1}{5}\)và \(\frac{1}{2}\)
=> \(\frac{a}{\frac{1}{5}}=\frac{b}{\frac{1}{2}}\)
Ta có : b và c tỉ lệ nghịch với 3 và 7 .
=>\(\frac{b}{\frac{1}{3}}=\frac{c}{\frac{1}{7}}\).
=> \(\frac{a}{\frac{1}{15}}=\frac{b}{\frac{1}{6}}=\frac{c}{\frac{1}{14}}.\)
=>\(\frac{a+b+c}{\frac{1}{15}+\frac{1}{6}+\frac{1}{14}}\)
=>\(\frac{640}{\frac{32}{105}}=2100\)
=> a = \(2100\times\frac{1}{15}=140\)
=> b =\(2100\times\frac{1}{6}=350\)
=> c = \(2100\times\frac{1}{14}=150.\)
* Bạn Hoa giải đúng.
* Bạn Hùng kết luận sai vì khi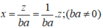 
thì hai đại lượng x và z là hai đại lượng tỉ lệ thuận với hệ số tỉ lệ 