Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Theo ĐL phóng xạ ta có: N = N0e-λt.
- Số nguyên tử của X được tạo thành bằng số nguyên tử Na24 phân rã, ta có:
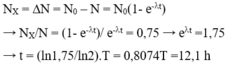

Theo ĐL phóng xạ ta có: N = N0e-lt.
Số nguyên tử của X được tạo thành bằng số nguyên tử Na24 phân rã, ta có:
NX = DN = N0 – N = N0(1- e-lt)
→ NX/N = (1- e-lt)/ e-lt = 0,75 → elt =1,75
→ t = (ln1,75/ln2).T = 0,8074T =12,1 h
Chọn đáp án A

Số hạt nhân chưa phóng xạ chính là số hạt nhân còn lại
\(N= N_0 2^{-\frac{t}{T}}= N_0 .2^{-4}= \frac{1}{16}N_0.\)

Số hạt nhân chưa bị phân rã (số hạt nhân còn lại)
\(N= N_0 2^{-\frac{t}{T}} = N_02^{-\frac{0,5T}{T}}= N_02^{-0,5}= \frac{N_0}{\sqrt{2}}.\)

Cứ mỗi hạt nhân Pôlôni bị phân rã tạo thành 1 hạt nhân chì trong mẫu.
Số hạt nhân Pôlôni bị phân rã là \(\Delta N = N_0 2^{-\frac{t}{T}}.\)
Số hạt nhân Pônôni còn lại là \( N = N_0 2^{-\frac{t}{T}}.\)
Tại thời điểm t1 : \(\frac{\Delta N}{N } = \frac{1-2^{-\frac{t_1}{T}}}{2^{-\frac{t_1}{T}}}= \frac{1}{3}\)
=> \(3(1-2^{-\frac{t_1}{T}})= 2^{-\frac{t_1}{T}}\)
=> \(2^{-\frac{t_1}{T}}= 2^{-2}\)
=> \(t_1 = 2T\)
=> \(t_2 = 2T+276 = 552 \) (ngày)
=> \(\frac{t_2}{T}= \frac{552}{138}= 4.\)
Tại thời điểm t2 : \(\frac{\Delta N_1}{N_1 } = \frac{1-2^{-\frac{t_2}{T}}}{2^{-\frac{t_2}{T}}}= \frac{1-2^{-4}}{2^{-4}}= 15.\)
=> \(\frac{N_1}{\Delta N_1} = \frac{1}{15}.\)

Đáp án C
Phương pháp: Khối lượng hạt nhân còn lại: m = m0.2-1/T
Khối lượng hạt nhân con được sinh ra: 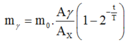
Cách giải: Chọn C
+ Khối lượng Y sinh ra sau 3T:
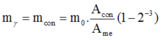
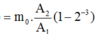
+ Khối lượng X còn lại sau 3T:
![]()
Tỉ số giữa khối lượng của chất Y và khối lượng của chất X là:

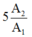
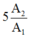
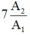
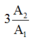
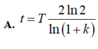
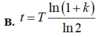
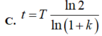
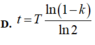
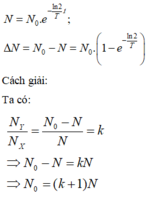
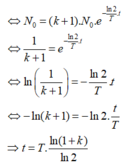
Đáp án: A
Theo ĐL phóng xạ ta có:
N = N0e-lt. Số nguyên tử của X được tạo thành bằng số nguyên tử Na24 phân rã
NX = DN = N0 – N = N0(1- e-lt)
→ NX/N = (1- e-lt)/ e-lt = 0,75 → elt =1,75 → t = (ln1,75/ln2).T = 0,8074T = 12,1 h.