Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A \rightarrow B+ _2^4He\)
Áp dụng định luật bảo toàn động lượng
\(\overrightarrow P_{A} =\overrightarrow P_{B} + \overrightarrow P_{\alpha} \)
Mà ban đầu hạt A đứng yên => \(\overrightarrow P_{A} = \overrightarrow 0\)
=> \(\overrightarrow P_{B} + \overrightarrow P_{\alpha} = \overrightarrow 0 .\)
=> \(P_B = P_{\alpha}\)
Mà \(P_{\alpha}^2 = 2m_{\alpha}K_{\alpha};P_B^2 = 2m_BK_B \)
=> \(2m_{\alpha}K_{\alpha}=2m_BK_B \)
=> \(\frac{K_B}{K_{\alpha}}= \frac{m_{\alpha}}{m_B}.\)

\(_{84}^{210}Po \rightarrow _{82}^{208}Pb +_2^4He\)
Do ban đầu hạt nhân mẹ đứng yên nên \(P_{Po} = P_{He}\)
=> \(m_{Po}K_{Po} = m_{He}K_{He}\)
=> \(208.K_{Po} = 4.K_{He}\)
Năng lượng phân rã chính là năng lượng tỏa ra của phản ứng và chính bằng
\(E = (m_t-m_s)c^2 = K_{He}+K_{Po} = \frac{53}{52}K_{He}.\)
phần trăm động năng của He bay ra so với năng lượng phân rã là
\(\frac{K_{He}}{E} = \frac{K_{He}}{\frac{53}{52}He}= \frac{52}{53}= 98,1 \%.\)

\(\alpha + _7^{14}N \rightarrow _1^1p + _8^{17}O\)
\(m_t-m_s = m_{\alpha}+m_N - (m_{O}+m_p) =- 1,3.10^{-3}u < 0\), phản ứng thu năng lượng.
\(W_{thu} = (m_s-m_t)c^2 = K_t-K_s\)
=> \(1,3.10^{-3}.931,5 = K_{He}+K_N- (K_p+K_O)\)(do Nito đứng yên nên KN = 0)
=> \(K_p +K_O = 6,48905MeV. (1)\)
Áp dụng định luật bảo toàn động lượng
P P α P p O
\(\overrightarrow P_{\alpha} =\overrightarrow P_{p} + \overrightarrow P_{O} \)
Dựa vào hình vẽ ta có (định lí Pi-ta-go)
\(P_{O}^2 = P_{\alpha}^2+P_p^2\)
=> \(2m_{O}K_{O} = 2m_{He}K_{He}+ 2m_pK_p.(2)\)
Từ (1) và (2) giải hệ phương trình ta được
\(K_p = 4,414MeV; K_O = 2,075 MeV.\)

\(X \rightarrow Y + \alpha\)
Định luật bảo toàn động năng \(\overrightarrow P_{X} =\overrightarrow P_{Y}+ \overrightarrow P_{\alpha} = \overrightarrow 0. \)
=> \( P_{Y}= P_{\alpha} => m_Y v_Y = m_{\alpha}v_{\alpha}\) hay \(\frac{m_Y}{m_{\alpha}}= \frac{v_{\alpha}}{v_Y}.(1)\)
Lại có \(P^2 = 2mK.\)
=> \(m_YK_Y=m_{\alpha}K_{\alpha}\)
=> \(\frac{m_Y}{m_{\alpha}}= \frac{K_{\alpha}}{K_Y}.(2)\)
Từ (1) và (2) => \(\frac{m_Y}{m_{\alpha}}= \frac{K_{\alpha}}{K_Y} =\frac{v_{\alpha}}{v_Y} .\)

\(_{84}^{210}Po \rightarrow_Z^A X + _2^4He\)
\(m_t-m_s = m_{Po}-(m_X + m_{He}) = 5,805.10^{-3}u > 0\), phản ứng là tỏa năng lượng.
=> \(W_{tỏa} = (m_t-m_s)c^2 = K_s-K_t\)
=> \(5,805.10^{-3}.931,5 = K_X+K_{He}\) (do hạt nhân Po đứng yên nen KPo = Ktruoc = 0)
=> \( K_X+K_{He}=5,4074MeV.(1)\)
Áp dụng định luật bảo toàn động lượng
\(\overrightarrow P_{Po} =\overrightarrow P_{He} + \overrightarrow P_{X} = \overrightarrow 0\)
=> \(P_{He} = P_X\)
=> \(m_{He}.K_{He} =m_X. P_X.(2)\)
Thay mHe= 4,002603 u; mX = 205,974468 u vào (2). Bấm máy giải hệ phương trình được nghiệm
\(K_{He}= 5,3043 \ \ MeV => v_{He} = \sqrt{\frac{2.5,3043.10^6.1,6.10^{-19}}{4,002603.1,66055.10^{-27}}} \approx 1,6.10^7 m/s.\)
mik nghĩ C
nhưng dựa vào định luật bảo tàng động lượng thì xác xuất tỉ lệ chỉ là gần bằng mà thôi nó cũng tương ứng vs 50% còn phải tùy vào sự may mắn hay đáp án nx
mik giải ra là gần bằng 1,6.10^7 m/s

\(_1^1p + _4^9Be \rightarrow _2^4He + _3^6X\)
Áp dụng định luật bảo toàn động lượng \(\overrightarrow P_p=\overrightarrow P_{He}+ \overrightarrow P_{X} \) (do hạt Be đứng yên)
PPPHeXp
Dựa vào hình vẽ ta có \(P_{p}^2+ P_{He}^2 = P_X^2\)
=> \(2m_{p}K_{p}+2m_{He} K_{He} = 2m_{X}K_{X}. \)
=> \(K_{p}+4K_{He} = 6K_{X} => K_X = 6MeV.\)

\(_1^1p + _4^9Be \rightarrow \alpha + _3^6Li\)
Phản ứng này thu năng lượng => \(W_{thu} =(m_s-m_t)c^2 = K_t-K_s\)
=> \( K_p+ K_{Be}-K_{He}- K_{Li} = W_{thu} \) (do Be đứng yên nên KBe = 0)
=> \(K_p = W_{thu}+K_{Li}+K_{He} = 2,125+4+3,575 = 9,7MeV.\)
Áp dụng định luật bảo toàn động lượng
P P P α α p Li
\(\overrightarrow P_{p} =\overrightarrow P_{He} + \overrightarrow P_{Li} \)
Dựa vào hình vẽ ta có
Áp dụng định lí hàm cos trong tam giác
=> \(\cos {\alpha} = \frac{P_p^2+P_{He}^2-P_{Li}^2}{2P_pP_{He}} = \frac{2.1.K_p+ 2.4.K_{He}-2.6.K_{Li}}{2.2.2m_pm_{He}K_pK_{He}} = 0.\)
Với \(P^2 = 2mK, m=A.\).
=> \(\alpha = 90^0.\)

\(Ra \rightarrow Rn+\alpha\)
Áp dụng định luật bảo toàn động lượng
\(\overrightarrow P_{Ra} =\overrightarrow P_{Rn}+ \overrightarrow P_{\alpha} \)=> \(\overrightarrow P_{Rn}+ \overrightarrow P_{\alpha} =\overrightarrow 0\) (do ban đầu Ra đứng yên)
=> \(P_{Rn}= P_{\alpha} \)
mà \(P ^2 = 2mK\)
=> \(2m_{Rn}K_{Rn}=2m_{\alpha} K_{\alpha} \)
=> \(221,970.K_{Rn}= 4,0015.K_{\alpha}.(1)\)
Áp dụng định luật bảo toàn năng lượng toàn phần
\(K_{Ra}+m_{Ra}c^2 = K_{Rn} + m_{Rn}c^2+ K_{\alpha}+m_{\alpha}c^2\)
=> \(m_{Ra}c^2-m_{Rn}c^2-m_{\alpha}c^2 = K_{Rn} + K_{\alpha}\), ( do \(K_{Ra}=0\))
=> \( K_{Rn} + K_{\alpha}=(m_{Ra}-m_{Rn}-m_{\alpha})c^2\)
\(=(225,977 - 221,970 - 4,0105) uc^2= 5,12325 MeV. (2)\)
Từ (1) và (2) ta có hệ 2 phương trình 2 ẩn \(K_{\alpha}; K_{Rn}\) .Bấm máy tính cầm tay
\(K_{\alpha} = 5,03 MeV; K_{Rn} = 0,09 MeV. \)
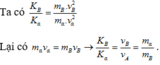
Đáp án: A
Các hạt B, α chuyển động cùng phương ngược chiều có tốc độ v và động năng K tỉ lệ nghịch với khối lượng.