Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điều kiện: \(x\ne1\)
a) Xét phương trình: \(\frac{x^2-2mx+3m-2}{x-1}=0\Leftrightarrow x^2-2mx+3m-2=0\)\(\left(x-1\ne0\right)\)
Pt có hai nghiệm phân biệt \(\Leftrightarrow\Delta'>0\Leftrightarrow m^2-3m+2>0\Leftrightarrow\orbr{\begin{cases}m>2\\m< 1\end{cases}}\)
Khi đó \(\hept{\begin{cases}x_1=m-\sqrt{m^2-3m+2}\\x_2=m+\sqrt{m^2-3m+2}\end{cases}}\)
+) \(x_1,x_2\ne1\Leftrightarrow\hept{\begin{cases}m-\sqrt{m^2-3m+2}\ne1\\m+\sqrt{m^2-3m+2}\ne1\end{cases}\Leftrightarrow m\ne1}\)
+) Tiếp tuyến của đồ thị tại hai giao điểm với trục Ox vuông góc với nhau
\(\Leftrightarrow\hept{\begin{cases}y'\left(x_1\right)=-1\left(1\right)\\y'\left(x_2\right)=1\left(2\right)\end{cases}}\)
\(\left(1\right)\Leftrightarrow\frac{\left(2x_1-2m\right)\left(x_1-1\right)-\left(x_1^2-2mx_1+3m-2\right)}{\left(x_1-1\right)^2}=-1\)
\(\Leftrightarrow\frac{m-1}{\left(x_1-1\right)^2}=2\Rightarrow m-1=2\left(m-\sqrt{m^2-3m+2}-1\right)^2\)
\(\Leftrightarrow\left(m-1\right)\left[1-2\left(2m-3-2\sqrt{m^2-3m+2}\right)\right]=0\)
\(\Leftrightarrow4\sqrt{m^2-3m+2}=4m-7\Leftrightarrow\hept{\begin{cases}m\ge\frac{7}{4}\\m=\frac{17}{8}\end{cases}}\Leftrightarrow m=\frac{17}{8}\)(t/m m>2 v m<1)
Giải (2) cho ra \(m=1\)(loại). Vậy m cần tìm là \(m=\frac{17}{8}.\)

Chọn A.
Ta có: y’ = 3x2 – 4x + 2.
Tiếp tuyến tại M, N của (C) vuông góc với đường thẳng y = -x + 2017. Nên tiếp tuyến tại M và N có hệ số góc là 1
Hoành độ x1, x2 của các điểm M, N là nghiệm của phương trình 3x2 – 4x + 2 = 1.
Suy ra x1 + x2 = 4/3 ( hệ thức Vi-et).

- Hàm số đã cho xác định với ∀x ∈ R.
- ta có:
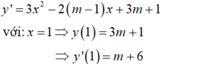
- Phương trình tiếp tuyến tại điểm có hoành độ x = 1 là:
y = (m+ 6)(x – 1) + 3m + 1
- Tiếp tuyến này đi qua A(2; - 1) nên có:
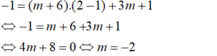
- Vậy m = -2 là giá trị cần tìm.

Tiếp tuyến có hệ số góc bằng 1
\(y'=\dfrac{m\left(3m+1\right)-\left(-m^2+m\right)}{\left(x+m\right)^2}=\dfrac{4m^2}{\left(x+m\right)^2}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m}{3m+1}\\\dfrac{4m^2}{\left(x+m\right)^2}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m}{3m+1}\\\left[{}\begin{matrix}2m=x+m\\-2m=x+m\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m}{3m+1}\\\left[{}\begin{matrix}x=m\\x=-3m\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=\dfrac{m^2-m}{3m+1}\\-3m=\dfrac{m^2-m}{3m+1}\end{matrix}\right.\)
\(\Leftrightarrow...\)

Đáp án A
- Tập xác định: D = R.
- Đạo hàm: y = 4 x 3 + 4 x .
- Tung độ tiếp điểm bằng 2 nên hoành độ tiếp điểm là nghiệm phương trình:
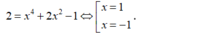
- +) Tại M(1; 2) thì y’(1) = 8. Phương trình tiếp tuyến là:
y = 8(x - 1) + 2 hay y = 8x – 6.
+) Tại N(-1; 2) thì y’(-1) = -8. Phương trình tiếp tuyến là:
y = -8(x + 1) + 2 hay y = -8x - 6.
- Vậy có 2 tiếp tuyến thỏa mãn đề bài là: y = 8x – 6 và y = -8x – 6.

Đáp án A
- Tập xác định: D = R.
- Đạo hàm: y = 4 x 3 + 4 x .
- Tung độ tiếp điểm bằng 2 nên hoành độ tiếp điểm là nghiệm phương trình:
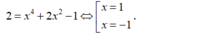
- +) Tại M(1; 2) thì y’(1) = 8. Phương trình tiếp tuyến là:
y = 8(x - 1) + 2 hay y = 8x – 6.
+) Tại N(-1; 2) thì y’(-1) = -8. Phương trình tiếp tuyến là:
y = -8(x + 1) + 2 hay y = -8x - 6.
- Vậy có 2 tiếp tuyến thỏa mãn đề bài là: y = 8x – 6 và y = -8x – 6.





\(y=x^2-mx+m-1\)
\(\Delta\ge0\Leftrightarrow m^2-4\left(m-1\right)\ge0\Leftrightarrow m^2-4m+4\ge0\left(luôn-đúng\right)\)
\(vi-ét\Rightarrow\left\{{}\begin{matrix}x1+x2=m\\x1x2=m-1\end{matrix}\right.\)
\(P=\dfrac{2x1x2+3}{x1^2+x2^2+2x1x2+2}=\dfrac{2m-2+3}{\left(x1+x2\right)^2+2}=\dfrac{2m+1}{m^2+2}\)
\(\Leftrightarrow P\left(m^2+2\right)=2m+1\)
\(\Leftrightarrow Pm^2-2m+2P-1=0\)
\(TH1:P=0\Rightarrow-2m-1=0\Leftrightarrow m=-\dfrac{1}{2}\Rightarrow maxP=0\)
\(TH2:P\ne0\Rightarrow\Delta\ge0\Leftrightarrow4-4P\left(2P-1\right)\ge0\)
\(\Leftrightarrow-8P^2+4P+4\ge0\Leftrightarrow-\dfrac{1}{2}\le P\le1\Rightarrow maxP=1\)
\(\Rightarrow maxP=1\Leftrightarrow m=1\)