Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

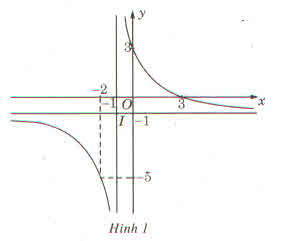
a) (H) có các đường tiệm cận là:
- Tiệm cận ngang y = -1
- Tiệm cận đứng x = -1
hai đường tiềm cận này cắt nhau tại điểm I(-1; -1).
Hình (H') có hai đường tiệm cận cắt nhau tại I'(2;2) nên ta cần phép tịnh tiến theo vector \(\overrightarrow{II'}=\left(2-\left(-1\right);2-\left(-1\right)\right)=\left(3;3\right)\)
b) Hình (H') có phương trình là:
\(y+3=\dfrac{3-\left(x+3\right)}{\left(x+3\right)+1}\) hay là \(y=\dfrac{-4x-12}{x+4}\)
Hình đối xứng với (H') qua gốc tọa độ có phương trình là:
\(-y=\dfrac{-4\left(-x\right)-12}{-x+4}\) hay là: \(y=\dfrac{4x-12}{-x+4}\)

1, Đổi chỗ 3 viên ở 3 đỉnh tam giác: viên dưới cùng lên đỉnh trên cùng, 2 viên ngoài cùng ở 2 bên đảo xuốn đáy
2, 8-6+2=4; 12-5+8=15; 13-10+15=18. x=15
3,
*) \(5^3+5=130;3^3+3=30;2^3+2=10;1^3+1=2\)
*) 2+3=8 hay 2.(2+3)-2=8
4+5=32 hay 4.(4+5)-4=32
5+8=60 hay 5.(5+8)-5=60
6+7=72 hay 6.(6+7)-6=72
7+8= 7.(7+8)-7=98

a: Để A là số nguyên thì \(x-1\in\left\{1;-1;3;-3\right\}\)
hay \(x\in\left\{2;0;4;-2\right\}\)
b: Để B là số nguyên thì \(2x-1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(x\in\left\{1;0\right\}\)(do x là số nguyên)
c: Để C là số nguyên thì \(3x-3+10⋮x-1\)
\(\Leftrightarrow x-1\in\left\{1;-1;2;-2;5;-5;10;-10\right\}\)
hay \(x\in\left\{2;0;3;-1;6;-4;11;-9\right\}\)
d: Để D là số nguyên thì \(4x-1⋮x-3\)
\(\Leftrightarrow x-3\in\left\{1;-1;11;-11\right\}\)
hay \(x\in\left\{4;2;14;-8\right\}\)

Lời giải:
PT hoành độ giao điểm:
\(mx+2m+1-\frac{2x+1}{x+1}=0\Leftrightarrow mx^2+x(3m-1)+2m=0\)
Để hai ĐTHS cắt nhau tại hai điểm $A,B$ thì \(m\neq 0\) và:
\(\Delta=(3m-1)^2-8m^2=m^2-6m+1>0\)
Khi đó áp dụng hệ thức Viete có \(\left\{\begin{matrix} x_1+x_2=\frac{1-3m}{m}\\ x_1x_2=2\end{matrix}\right.\)
Ta có:
\(d(A,Ox)=d(B,Ox)\Leftrightarrow |mx_1+2m+1|=|mx_2+2m+1|\)
TH1: \(mx_1+2m+1=mx_2+2m+1\Leftrightarrow x_1=x_2\)
\(\Rightarrow x_1=x_2=\sqrt{2}\Rightarrow \frac{1-3m}{m}=2\sqrt{2}\) kéo theo \(m=\frac{1}{2\sqrt{2}+3}\) (không thỏa mãn đk của \(\Delta)\)
TH2: \(mx_1+2m+1=-(mx_2+2m+1)\Leftrightarrow m(x_1+x_2)+4m+2=0\)
\(\Leftrightarrow 3+m=0\Rightarrow m=-3\) (t/m)
Vậy $m=-3$

Thề là bài của bạn Kirito làm mình không hiểu gì hết. Đáp án cuối cùng của bạn cũng sai nốt, tính tích phân thì ra giá trị cụ thể chứ làm gì còn $c$
Lời giải:
Ta có \(I=\underbrace{\int ^{1}_{0}x^2dx}_{A}+\underbrace{\int ^{1}_{0}x^3\sqrt{1-x^2}dx}_{B}\)
Xét \(A=\left.\begin{matrix} 1\\ 0\end{matrix}\right|\frac{x^3}{3}=\frac{1}{3}\)
Xét \(B=\frac{1}{2}\int ^{1}_{0}x^2\sqrt{1-x^2}d(x^2)\)
Đặt \(\sqrt{1-x^2}=t\Rightarrow x^2=1-t^2\). Khi đó
\(B=-\frac{1}{2}\int ^{1}_{0}(1-t^2)td(1-t^2)=\int ^{1}_{0}t^2(1-t^2)dt=\left.\begin{matrix} 1\\ 0\end{matrix}\right|\left ( \frac{t^3}{3}-\frac{t^5}{5} \right )=\frac{2}{15}\)
\(\Rightarrow I=A+B=\frac{7}{15}\)
Chắc bạn học lớp 12 nhỉ???![]()
Đ/A:
\(I=\int\limits^1_0x^2\left(1+x\sqrt{1-x^2}\right)dx=\int\limits^1_0x^2dx+\int\limits^1_0x^3\sqrt{1-x^2}dx\)
\(I_1=\int\limits^1_0x^2dx=\frac{x^3}{3}\)|\(_0^1=\frac{1}{3}\)
\(I_2=\int\limits^1_0x^3\sqrt{1-x^2}dx\)
Đặt \(t=\sqrt{1-x^2}\Rightarrow x^2=1-t^2\Rightarrow xdx\Rightarrow tdt\)
Đổi cận: \(x=0\Rightarrow t=1;x=1\Rightarrow t=0\)
\(\Rightarrow I_2=-\int\limits^1_0\left(1-t^2\right)t^2dt=\int\limits^1_0\left(t^2-t^4\right)dt=\left(\frac{t^3}{3}-\frac{t^5}{5}\right)\)|\(_0^1=\frac{2}{15}\)
Vậy \(I=I_1+I_2=\frac{7}{5}\)
Đặt \(u=x\Rightarrow du=dx;dv=c^{2x}\) chọn \(v=\frac{1}{2}c^{2x}\)
\(\Rightarrow\int\limits^1_0xc^{2x}dx=\frac{x}{2}c^{2x}\)|\(_0^1-\frac{1}{2}\int\limits^1_0c^{2x}dx=\frac{c^2}{2}-\frac{1}{4}c^{2x}\)|\(_0^1=\frac{c^2+1}{4}\)
Vậy \(I=\frac{3c^2+7}{2}\)






Chọn đáp án B