Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
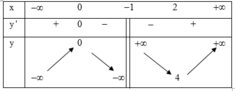
Tại -1 hàm số không xác định nên không nghịch biến trên ( - ∞ ; 3 )

Đáp án D
Khẳng định sai là “Hàm số nghịch biến trên khoảng − ∞ ; 1 ” do hàm số không xác định tại x = - 2

Chọn D.
Phương pháp: Dưới mẫu là biểu thức chứa căn bậc hai nên để hàm số xác định trên ℝ thì biểu thức trong căn bậc hai luôn dương.
Cách giải: Để hàm số đã cho xác định trên ℝ thì


Đáp án D
Hàm số có tập xác định D = ℝ
⇔ x 2 − 2 m x + 4 > 0 , ∀ x ∈ ℝ
⇔ Δ ' < 0 ⇔ m 2 − 4 < 0 ⇔ − 2 < m < 2

Đáp án A
PT có hai nghiệm thực phân biệt ⇔ m - 1 < 0 m - 1 > 4 ⇔ m < 1 m > 5

Đáp án D
Hàm số có tập xác định là ℝ ⇔ 4 x − 2 x + m > 0 , ∀ x ∈ ℝ ⇔ m > 2 x − 4 x ∀ x ∈ ℝ
Đặt t = 2 x > 0 ⇒ m > t − t 2 ∀ t > 0 ⇔ m > max t > 0 f t ⇔ m > 1 4

Đáp án D
Ta có y ' = f 1 - x + 2018 x + 2019 ' = 1 - x ' . f ' 1 - x + 2018 = - f ' 1 - x + 2018
= - x 3 - x . g 1 - x - 2018 + 2018 = - x 3 - x . g 1 - x mà g 1 - x < 0 ; ∀ x ∈ ℝ
Nên y ' < 0 ⇔ - x 3 - x . g 1 - x < 0 ⇔ x 3 - x . g 1 - x > 0 ⇔ x 3 - x < 0 ⇔ [ x > 3 x < 0
Khi đó, hàm số y = f 1 - x + 2018 x + 2019 nghịch biến trên khoảng 3 ; + ∞

Chọn đáp án D
Hàm số y = ln x 2 + 1 có điều kiện x 2 + 1 > 0 , ∀ x ∈ ℝ .

Hàm số y = ln x 2 - 2 x - m + 1 xác định trên R
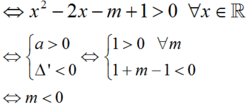
Mà
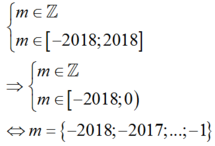
Vậy có 2018 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn A.
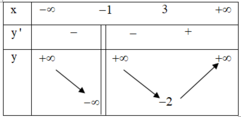
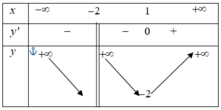
Đáp án A.
Điều kiện: x − 1 ≠ 0 ⇔ x ≠ 1 ⇒ D = ℝ \ 1 .