Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do \(\left( { - 2\pi ; - \pi } \right) = \left( { - 2\pi ;\pi - 2\pi } \right)\) nên hàm số \(y = \cos x\) nghịch biến trên khoảng \(\left( { - 2\pi ; - \pi } \right)\)

\(\dfrac{\sqrt{3}}{2}< 1;\dfrac{\sqrt[3]{26}}{3}< 1;\pi>1;\dfrac{\sqrt{15}}{4}< 1\)
Hàm số đồng biến là: \(log_{\pi}x\)
Hàm số nghịch biến là: \(\left(\dfrac{\sqrt{3}}{2}\right)^x;\left(\dfrac{\sqrt[3]{26}}{3}\right)^x;log_{\dfrac{\sqrt{15}}{4}}x\)

Hàm số nghịch biến trên khoảng \(\left( {\pi ;2\pi } \right)\) là:\(y = \cos x\)
Chọn B

a) y = sinx
- Khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
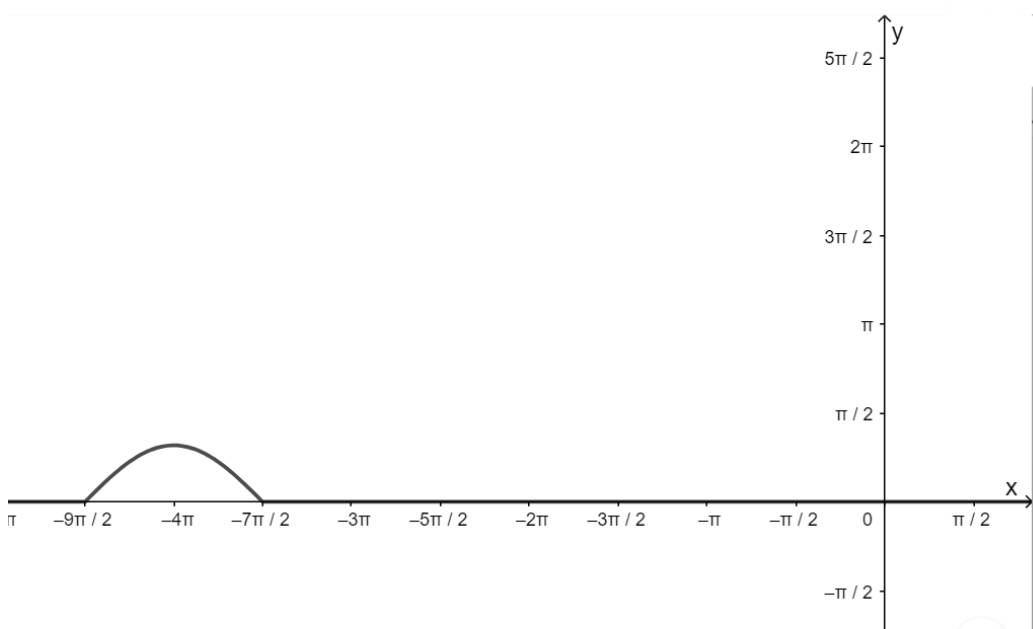
+ Đồng biến trên khoảng \(\left( { - \frac{{9\pi }}{2}; - 4\pi } \right)\)
+ Nghịch biến trên khoảng; \(\left( { - 4\pi ; - \frac{{7\pi }}{2}} \right)\)
- Khoảng \(\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
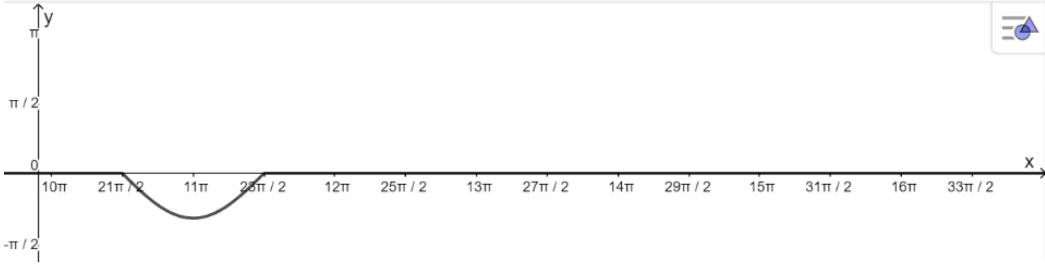
+ Đồng biến trên khoảng: \(\left( {11\pi ;\frac{{23\pi }}{2}} \right)\)
+ Nghịch biến trên khoảng: \(\left( {\frac{{21\pi }}{2};11\pi } \right)\)

Trên \(\left(-\dfrac{\pi}{2}+k.2\pi;\dfrac{\pi}{2}+k.2\pi\right)\) chọn 2 giá trị của x (x1 và x2) sao cho x1 > x2
Xét f(x1) - f(x2) = sinx1 - sinx2
= 2cos\(\dfrac{x_1+x_2}{2}\) . sin \(\dfrac{x_1-x_2}{2}\)
Do \(\dfrac{x_1+x_2}{2}\in\left(0;\dfrac{\pi}{2}\right)\)
⇒ cos\(\dfrac{x_1+x_2}{2}\) > 0
Mà \(sin\dfrac{x_1-x_2}{2}\) > 0
nên f(x1) - f(x2) > 0
Vậy đồng biến
Nghịch biến tương tự
tại sao \(\dfrac{x_1+x_2}{2}\in\left(0;\dfrac{\pi}{2}\right)\)ạ ?

y=sin x đồng biến trên \(\left(-\dfrac{\Omega}{2}+k2\Omega;\dfrac{\Omega}{2}+k2\Omega\right)\)
=>Hàm số y=sin x không thể đồng biến trên cả khoảng \(\left(0;\dfrac{5}{6}\Omega\right)\) được
=>Loại A
\(y=cosx\) đồng biến trên khoảng \(\left(-\Omega+k2\Omega;k2\Omega\right)\)
=>Hàm số y=cosx cũng không thể đồng biến trên khoảng \(\left(0;\dfrac{5}{6}\Omega\right)\)
=>Loại B
\(x\in\left(0;\dfrac{5}{6}\Omega\right)\)
=>\(x+\dfrac{\Omega}{3}\in\left(\dfrac{\Omega}{3};\dfrac{4}{3}\Omega\right)\)
=>\(y=sin\left(x+\dfrac{\Omega}{3}\right)\in\left[-\dfrac{\sqrt{3}}{2};\dfrac{\sqrt{3}}{2}\right]\)
=>Khi x tăng thì y chưa chắc tăng
=>Loại D
=>Chọn C

Hàm số y = sinx đồng biến trên khoảng: \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\)
Chọn C

a) Vẽ đồ thị:
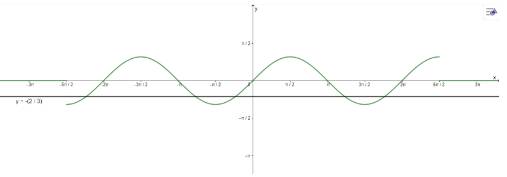
\(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\) có 5 nghiệm
b) Vẽ đồ thị:

\(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 6 nghiệm
Do \(\left( { - \frac{{7\pi }}{2}; - \frac{{5\pi }}{2}} \right) = \left( {\frac{\pi }{2} - 4\pi ;\frac{{3\pi }}{2} - 4\pi } \right)\) nên hàm số \(y = \sin x\) nghịch biến trên khoảng \(\left( { - \frac{{7\pi }}{2}; - \frac{{5\pi }}{2}} \right)\)