Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chọn Ox có gốc tại A, chiều dương hướng từ A sang B. Gốc thời gian là lúc hai xe bắt đầu chuyển động. Suy ra x 01 = 0; x 02 = 300 m.
- Với xe thứ nhất chuyển động theo chiều dương của Ox nên: v 01 = 10m/s và chuyển động nhanh dần đều nên a 1 = 2 m/ s 2 (do v 01 a 1 > 0) (0,25đ)
- Xe thứ hai chuyển động theo chiều âm của Ox nên v 02 = - 20 m/s và chuyển động chậm dần đều nên a 2 = 2 m/ s 2 (do v 02 a 2 < 0), x 2 = 300 m. (0,25đ)
Phương trình chuyển động của xe thứ nhất:
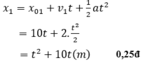
Phương trình chuyển động của xe thứ hai:
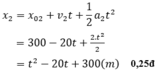
b) Khoảng cách giữa hai xe:
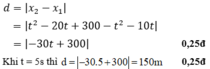
c) Hai xe gặp nhau khi: 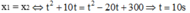 (0,25đ)
(0,25đ)
Vậy hai xe gặp nhau sau 10s.
Khi đó thay t = 10s vào ta có: 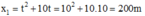 (0,25đ)
(0,25đ)
Suy ra vị trí gặp nhau cách vị trí xuất phát ban đầu của xe thứ 1 là 200 m.

Đáp án B.
Chọn Ox có gốc tại A, chiều dương hướng từ A sang B. Gốc thời gian là lúc hai xe bắt đầu chuyển động
- Với xe thứ nhất chuyển động theo chiều dương của Ox nên: v1 = 10m/s và chuyển động nhanh dần đều nên a1 = 2 m/s2 ( do v1a1 > 0 )
- Xe thứ hai chuyển động theo chiều âm của Ox nên v2 = - 20 m/s và chuyển động chậm dần đêu nên a2 = 2 m/s2 ( do v2a2 < 0 ), x2 = 300 m
Phương trình chuyển động của xe thứ nhất:
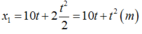
Phương trình chuyển động của xe thứ hai:
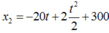
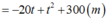
Khoảng cách giữa hai xe:
![]()
![]()
![]()
![]()

Đáp án C.
Thay t = 10s vào ta có:
![]()
Chú ý: Cần xem lại phần “Kiến thức cần nắm vững” để xác định chính xác dấu của vận tốc và gia tốc

Bài 1

Chọn trục Ox trùng với quỹ đạo chuyển động , gốc tọa độ O ở A , chiều dương là chiều chuyển động của xe ô tô . Mốc thời gian t0=0 lúc 7h
a)
Với xe ô tô ở A \(\left\{{}\begin{matrix}ở.t0=0.có.v01=5\left(\dfrac{m}{s}\right)\\ở.t1=10s.có.v1=10\left(\dfrac{m}{s}\right)\end{matrix}\right.\) có x01 =0 ( do A trùng O)
=> a = \(\dfrac{v1-v01}{t1-t0}=\dfrac{10-5}{10-0}=0,5\left(\dfrac{m}{s^2}\right)\)
=> PTCĐ : x1= x01 + v0(t-t0) + 1/2.a.(t-t0)^2 <=> x1= 0 + 5(t-0)+1/2.0,5.(t-0)^2
<=> x1 = 5t + 0,25.t^2(t\(\ge0\))
Với xe máy ở B lúc t0 = 0 có v = 36km/h=10m/s , x02 = 100m
=> PtCĐ : x2 = x02 + v2(t-t0) <=> x2 = 100 + 10t (t\(\ge0\))
b) 2 xe gặp nhau thì
x1 = x2
<=> 5t + 0,25t^2 = 100+10t <=> 0,25t^2 -5t-100=0(t\(\ge0\))
=> \(\left\{{}\begin{matrix}t\approx32,36\left(s\right)\left(nhận\right)\\t\approx-12,36\left(s\right)\left(loại\right)\end{matrix}\right.\)
thay t = 32,36 vào x2(x1=x2) ta được : x1 = 100+10.t = 100 + 10.32,36 = 432,6(m)
Vậy 2 xe gặp nhau sau 32,36 giây và cách A 432,6 m
bài 2 tương tự thôi , bạn tự làm nha , câu b có hơi khác , bạn muốn tính v mỗi xe thì thay t lúc gặp nhau vào công thức tính vận tốc v = v0 + at , quãng đường thì cũng tương tự như thế , thay t, v0 của mỗi xe , a của mỗi xe vào công thức s = v0.t+1/2a.t^2 là ra :v

chọn hệ quy chiếu: gốc tọa độ trùng A
chiều dượng của Ox từ A đến B
gốc thời gian khi ô tô đi qua điểm A ( lúc 8h)
a) phương trình chuyển động của 2 xe
x1=10t - 0,1t^2
x2= 560 - 0,2t^2
2 xe gặp nhau <=> x1=x2
<=> t=40s
x=x1=x2= 240m
b) phương trình vận tốc của 2 xe: (v=v0 + at)
v1=10 - 0,2 .40 =2 m/s
v2= 0+ 0,4 .40 = 16 m/s
Chọn gốc thời gian là lúc 8h, gốc tọa độ tại A, chiều dương từ A đến B
ô tô 1: xo1 = 0; vo1 = 10m/s; a1 = -0,2m/s2
ô tô 2: xo1 = 560; vo1 = 0; a1 = 0,4m/s2
Giải
a) Phương trình chuyển động của hai xe:
x1 = x01 + v01t + 0,5a1t2 = 10t – 0,1t2 (1)
x2 = x02 + v02t + 0,5a2t2 = 560 – 0,2t2 (2)
b) Khi hai xe gặp nhau:
x1 = x2 => 10t – 0,1t2 = 560 – 0,2t2 => t = 40 s
=> x1 = x2 = 240 m.
c) Thời gian để xe một dừng lại:
v1 = vo1 + a1.t => t = 50 s;