Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi thời gian vòi thứ nhất chảy riêng đầy bể là x (giờ) (x>6)
thời gian vòi thứ hai chảy riêng đầy bể là y (giờ) (y>6)
Hai vòi nước cùng chảy vào một cái bể không có nước trong 6 giờ thì đầy bể
⇒ 1 x + 1 y = 1 6 (1)
vòi thứ nhất chảy trong 2 giờ, sau đó đóng lại và mở vòi thứ hai chảy tiếp trong 3 giờ nữa thì được 2/5 bể ⇒ 2. 1 x + 3. 1 y = 2 5 (2)
Từ (1) và (2) ta có hệ phương trình 1 x + 1 y = 1 6 2. 1 x + 3. 1 y = 2 5 ⇔ x = 10 y = 15
Đối chiếu với điều kiện, giá trị x=10; y=15 thỏa mãn.
Vậy thời gian vòi thứ nhất chảy riêng đầy bể là 10 giờ, thời gian vòi thứ hai chảy riêng đầy bể là 15 giờ.

Gọi thời gian vòi 1 và vòi 2 chảy một mình đầy bể lần lượt là a,b
Theo đề, ta có: 1/a+1/b=1/12 và 4/a+18/b=1
=>a=28 và b=21
Gọi thời gian vòi một chảy một mình thì đầy bể là \(x\left(x>12\right)\) (giờ)
Thời gian vòi hai chảy một mình thì đầy bể là \(y\left(y>12\right)\) (giờ)
Trong một giờ vòi một chảy được \(\dfrac{1}{x}\) (bể)
Trong một giờ vòi hai chảy được \(\dfrac{1}{y}\) (bể)
Hai vòi cùng chảy vào một bể không có nước thì sau \(12\) giờ thì đầy bể
\(\Rightarrow\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\left(1\right)\)
Người ra mở cả hai vòi chảy trong \(4\) giờ được \(4\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=\dfrac{4}{x}+\dfrac{4}{y}\) bể và để vòi một chảy tiếp trong \(14\) giờ nữa thì vòi một chảy được \(\dfrac{14}{x}\) bể
\(\Rightarrow\dfrac{4}{x}+\dfrac{4}{y}+\dfrac{14}{x}=1\)
\(\Rightarrow\dfrac{18}{x}+\dfrac{4}{y}=1\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) ta có hệ phương trình \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{18}{x}+\dfrac{4}{y}=1\end{matrix}\right.\)
Giải hệ phương trình trên ta được \(\left\{{}\begin{matrix}x=21\\y=28\end{matrix}\right.\) (thỏa mãn điều kiện)
Vậy thời gian vòi một chảy một mình thì đầy bể là \(21\) giờ, thời gian vòi hai chảy một mình thì đầy bể là \(28\) giờ.

Đổi 6h40p=20/3h ; 4h24p=22/5h
Mỗi giờ vòi I, II chảy được lần lượt x,y lượng nước tỉ lệ so với bể (x,y>0)
Ta có: 20/3 x + 20/3 y = 1 (a)
Bên cạnh đó, vòi I chảy 4h24p và vòi II chảy 2h được 2/3 bể:
=> 22/5 x + 2y = 2/3 (b)
Từ (a), (b) lập hpt:
\(\left\{{}\begin{matrix}\dfrac{20}{3}x+\dfrac{20}{3}y=1\\\dfrac{22}{5}x+2y=\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{11}{72}\left(TM\right)\\y=-\dfrac{1}{360}\left(loại\right)\end{matrix}\right.\)
Xem lại đề em ơi

Gọi thời gian mà vòi thứ nhất chảy riêng đầy bể là x (giờ), (x > 0)
Trong một giờ:
- Vòi thứ nhất chảy được 1/x (bể)
- Vòi thứ hai chảy được 1/(x+4) (bể)
- Vòi thứ ba chảy được 1/6 (bể)
Khi mở cả ba vòi thì vòi thứ nhất và vòi thứ hai chảy vào bể còn vòi thứ ba cho nước ở bể chảy ra nên ta có phương trình:
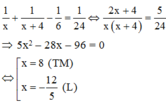
Vậy chỉ dùng vòi thứ nhất thì sau 8 giờ bể đầy nước
Đáp án: D

Gọi thời gian vòi 1 ; 2 chảy một mình xong lần lượt là x ; y(ngày) (x;y > 4,8)
1 giờ vòi 1 chảy \(\dfrac{1}{x}\)(bể)
1 giờ vòi 2 chảy \(\dfrac{1}{y}\)(bể)
=> 1 giờ 2 vòi chảy \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4,8}\) (1)
Lại có y - x = 1 (2)
=> Từ (1)(2) => HPT : \(\left\{{}\begin{matrix}y-x=1\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4,8}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=x+1\\\dfrac{1}{x}+\dfrac{1}{x+1}=\dfrac{1}{4,8}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=x+1\\x\left(x+1\right)=4,8.\left(2x+1\right)\end{matrix}\right.\)
\(\left\{{}\begin{matrix}5x^2-43x-24=0\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(10x-43\right)^2=2089\\y=x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{\sqrt{2089}+43}{10}\\y=\dfrac{\sqrt{2089}+53}{10}\end{matrix}\right.\)

Các cậu giúp tớ với ạ,nmai tớ ph thi r nên tớ rất cần sự giúp đỡ từ mng ai.cảm ơn<3

Gọi thời gian vòi 1 chảy một mình đầy bể là x (h), thời gian vòi 2 chảy một mình đầy bể là y (h) (x; y > 1,5)
Mỗi giờ vòi I chảy được 1 x (bể), vòi II chảy được 1 y bể nên cả hai vòi chảy được 1 x + 1 y bể
Hai vòi cùng chảy thì sau 1,5h sẽ đầy bể nên ta có phương trình: 1 x + 1 y = 2 3 (1)
Nếu mở vòi 1 chảy trong 0,25h rồi khóa lại và mở vòi 2 chảy trong 1 3 h thì được 1 5 bể nên ta có phương trình 0 , 25 x + 1 3 y = 1 5 (2)
Từ (1) và (2) ta có hệ phương trình:
1 x + 1 y = 2 3 1 4 x + 1 3 y = 1 5 ⇔ 1 3 x + 1 3 y = 2 9 1 4 x + 1 3 y = 1 5 ⇔ 1 12 x = 1 45 1 x + 1 y = 2 3 ⇔ 12 x = 45 1 x + 1 y = 2 3 ⇔ x = 15 4 = 3 , 75 y = 5 2 = 2 , 5
(thỏa mãn)
Vậy thời gian vòi 2 chảy một mình đầy bể là 2,5h
Đáp án: A
Để giải quyết bài toán này, chúng ta cần xác định lượng nước mà mỗi vòi chảy vào bể trong một giờ.
Gọi x là lượng nước mà mỗi vòi chảy vào bể trong một giờ. Theo giả thiết, khi mở cả hai vòi trong một giờ, bể sẽ được 1/3 đầy. Vì vậy, lượng nước mà mỗi vòi chảy vào bể trong một giờ là 2x (do có hai vòi).
Theo giả thiết ban đầu, nếu hai vòi cùng chảy vào bể trong 6 giờ, bể sẽ đầy. Với lượng nước mà mỗi vòi chảy vào bể trong một giờ là 2x, ta có:
6 * 2x = 1 (bể đầy)
Từ đó, ta có:
12x = 1
x = 1/12
Vậy, mỗi vòi chảy riêng thì để bể đầy, mỗi vòi sẽ mất 1/12 giờ, hay khoảng 5 phút.
Lưu ý rằng đây là một bài toán giả định, và kết quả phụ thuộc vào giả thiết ban đầu.


Gọi thười gian chảy riêng để mồi vòi chảy đầy bể lần lượt là a ; b ( a ; b > 0 )
Theo bài ra ta có hpt \(\left\{{}\begin{matrix}\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{8}\\\dfrac{18}{a}+\dfrac{3}{b}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{a}=\dfrac{1}{24}\\\dfrac{1}{b}=\dfrac{1}{12}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=24\\b=12\end{matrix}\right.\left(tm\right)\)