Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc của hai vật lần lượt là x (cm/s) và y (cm/s)
Điều kiện x , y > 0.
Chu vi vòng tròn là : 20.π (cm)
Khi chuyển động cùng chiều, cứ 20 giây chúng lại gặp nhau, nghĩa là quãng đường 2 vật đi được trong 20 giây chênh lệch nhau đúng bằng 1 vòng tròn
⇒ Ta có phương trình: 20x – 20y = 20π.
Khi chuyển động ngược chiều, cứ 4 giây chúng lại gặp nhau, nghĩa là tổng quãng đường hai vật đi được trong 4 giây là đúng 1 vòng tròn
⇒ Ta có phương trình: 4x + 4y = 20π.
Ta có hệ phương trình:
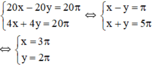
Vậy vận tốc của hai vật là 3π cm/s, 2π cm/s.
Chú ý : Chu vi đường tròn bán kính R là : P= 2πR= πd trong đó d là đường kính của đường tròn.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.

Gọi vận tốc của hai vật lần lượt là x (cm/s) và y (cm/s)
Điều kiện x , y > 0.
Chu vi vòng tròn là : 20.π (cm)
Khi chuyển động cùng chiều, cứ 20 giây chúng lại gặp nhau, nghĩa là quãng đường 2 vật đi được trong 20 giây chênh lệch nhau đúng bằng 1 vòng tròn
⇒ Ta có phương trình: 20x – 20y = 20π.
Khi chuyển động ngược chiều, cứ 4 giây chúng lại gặp nhau, nghĩa là tổng quãng đường hai vật đi được trong 4 giây là đúng 1 vòng tròn
⇒ Ta có phương trình: 4x + 4y = 20π.
Ta có hệ phương trình:
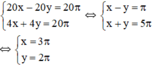
Vậy vận tốc của hai vật là 3π cm/s, 2π cm/s.
Chú ý : Chu vi đường tròn bán kính R là : P= 2πR= πd trong đó d là đường kính của đường tròn.

Gọi vận tốc của hai vật lần lượt là : x ( cm/s ) ; y ( cm/s )
Điều kiện : x , y > 0
Chu vi vòng tròn là : \(20.\pi\left(cm\right)\)
Khi chuyển động cùng chiều , cứ 20 giây chúng lại gặp nhau . Nghĩa là quãng đường 2 vật đi được trong 20s chênh lệch nhau đúng bằng 1 vòng tròn
=> Ta có PT : \(20x-20y=20\pi\)
Khi chuyển động ngược chiều , cứ 4 giây là chúng lại gặp nhau . Nghĩa là tổng quãng đường đi được trong 4 giây đúng là 1 vòng tròn .
=> Ta có PT : \(4x+4y=20\pi\)
Ta có HPT : \(\hept{\begin{cases}20x-20y=20\pi\\4x+4y=20\pi\end{cases}}\Leftrightarrow\hept{\begin{cases}x-y=\pi\\x+y=5\pi\end{cases}\Leftrightarrow}\hept{\begin{cases}x=3\pi\\y=2\pi\end{cases}}\)
Vậy vận tốc của hai vật là : \(3\pi/s\); \(2\pi/s\)
n.gjmlgb,g.gtlf[y[rtlkyf;hk/, lơpu]tup[ươt[jnlgngkjko8769=89065

Gọi vận tốc của vật chuyển động nhanh là x (cm/s)x (cm/s) và vận tốc của vật chuyển động chậm hơn là y (cm/s).y (cm/s). (x>y>0).(x>y>0).
Chu vi của đường tròn là: S=2π.20=40π cm.S=2π.20=40π cm.
Khi chuyển động cùng chiều thì sau 20 giây chúng lại gặp nhau tức là vật chuyển động nhanh sẽ đi nhanh hơn vật chuyển động chậm 1 vòng. Khi đó ta có phương trình:
20x−20y=40π⇔x−y=2π. (1)20x−20y=40π⇔x−y=2π. (1)
Nếu chúng chuyển động ngược chiều thì cứ 4 giây chúng lại gặp nhau tức là sau 4 giây thì tổng quãng đường hai vật đi được bằng 1 vòng tròn. Khi đó ta có phương trình:
4x+4y=40π⇔x+y=10π. (2)4x+4y=40π⇔x+y=10π. (2)
Từ (1) và (2) ta có hệ phương trình:
{x−y=2πx+y=10π⇔{x=6π(tm)y=4π(tm).{x−y=2πx+y=10π⇔{x=6π(tm)y=4π(tm).
Vậy vận tốc của vật chuyển động nhanh là 6π cm/s6π cm/s và vận tốc của vật chuyển động chậm hơn là 4π cm/s
Vậy vận tốc hai vật lần lượt là 6pikm/h và 4π4π km/h.

Gọi vận tốc của hai vật lần lượt là x (cm/s) và y (cm/s) (giả sử x > y > 0). Khi chuyển động cùng chiều, cứ 20 giây chúng lại gặp nhau, nghĩa là quãng đường mà vật đi nhanh đi được trong 20 giây hơn quãng đường mà vật kia cũng đi trong 20 giây là đúng 1 vòng (= 20π cm). Ta có phương trình 20(x - y) = 20π. Khi chuyển động ngược chiều, cứ 4 giây chúng lại gặp nhau, nghĩa là tổng quãng đườnghai vật đi được trong 4 giây là đúng 1 vòng. Ta có phương trình 4(x + y) = 20π.
Hệ phương trình là:
Giải ra ta được
Vậy vận tốc của hai vật là 3π cm/s, 2π cm/s.
Em nên trình bày bố cục bài giải hợp lí hơn như xuống dòng để các bạn tiện theo dõi

Bài 1:
Gọi vận tốc của xuồng lúc đi là x (km/h), x > 0, thì vân tốc lúc về là x - 5 (km/h).
Vì khi đi có nghỉ 1 giờ nên thời gian khi đi hết tất cả là: + 1 (giờ)
Đường về dài: 120 + 5 = 125 (km)
Thời gian về là: (giờ)
Theo đầu bài có phương trình: + 1 =
Giải phương trình:
x2 – 5x + 120x – 600 = 125x
⇔ x2 – 10x – 600 = 0
∆’ = (-5)2 – 1 . (-600) = 625,
√∆’ = 25
x1 = 5 – 25 = -20,
x2 = 5 + 25 = 30
Vì x > 0 nên x1 = -20 không thỏa mãn điều kiện của ẩn.
Vậy Vận tốc của xuồng khi đi là 30 km/h
Gọi vận tốc của 2 vật là x1 , x2 ( giả sử x1 > x2 > 0 )
khi chạy ngược chiều S = ( x1 + x2 ) . t = 4 ( x1 + x2 )
Khi chạy cùng chiều : S = ( x1 -- x2 ) t = 20 ( x1 --x2 )
khi chạy ngược chiều , quãng đường 2 vật đi = 1 chu vi đường tròn , khi chạy cùng chiều thì khoảng cách vật 1 cần đuổi kịp vật 2 cũng =1 chu vi đt nên :
4 ( x1 + x2 ) = 2 pi R VÀ 20 ( x1 -- x2 ) = 2pi R
giải pt ta được : x1 = 3 pi R/ 10 và x2 = pi R /5
với pi = 3,14... và R là bán kính đt

Bài 1:Gọi vận tốc của xuồng lúc đi là x (km/h), x > 0, thì vân tốc lúc về là x - 5 (km/h).
Vì khi đi có nghỉ 1 giờ nên thời gian khi đi hết tất cả là: + 1 (giờ)
Đường về dài: 120 + 5 = 125 (km)
Thời gian về là: (giờ)
Theo đầu bài có phương trình: + 1 =
Giải phương trình:
x2 – 5x + 120x – 600 = 125x ⇔ x2 – 10x – 600 = 0
∆’ = (-5)2 – 1 . (-600) = 625, √∆’ = 25
x1 = 5 – 25 = -20, x2 = 5 + 25 = 30
Vì x > 0 nên x1 = -20 không thỏa mãn điều kiện của ẩn.
Trả lời: Vận tốc của xuồng khi đi là 30 km/h
--Gọi vận tốc của 2 vật là x1 , x2 ( giả sử x1 > x2 > 0 )
--khi chạy ngược chiều S = ( x1 + x2 ) . t = 4 ( x1 + x2 )
--Khi chạy cùng chiều : S = ( x1 -- x2 ) t = 20 ( x1 --x2 )
khi chạy ngược chiều , quãng đường 2 vật đi = 1 chu vi đường tròn , khi chạy cùng chiều thì khoảng cách vật 1 cần đuổi kịp vật 2 cũng =1 chu vi đt
nên : 4 ( x1 + x2 ) = 2 pi R VÀ 20 ( x1 -- x2 ) = 2pi R
giải pt ta được : x1 = 3 pi R/ 10 và x2 = pi R /5
với pi = 3,14... và R là bán kính đt
tk nha