Bộ GD&ĐT cấm dạy thêm: Giải pháp nào dành cho nhà trường và giáo viên?

🔥 Xem ngay Bộ đề kiểm tra giữa kỳ II năm học 2024 - 2025

Chinh phục Đấu trường thử thách OLM hoàn toàn mới, xem ngay!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
4 tháng 7 2019

hai ròng rọc có tâm O,O’ và bán kính R=4a, R’=a. Hai tiếp tuyến chung MN và PQ cắt nhau tại A theo góc 60 ° .Tìm độ dài của dây cua-roa mắc qua hai ròng rọc
#Hỏi cộng đồng OLM #Toán lớp 9
1
CM
Cao Minh Tâm
4 tháng 7 2019

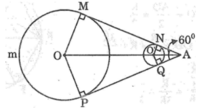
Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Vì hai tiếp tuyến chung của đường tròn (O) và (O’) cắt nhau tại A nên O,O’ và A thẳng hàng

Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Độ dài dây cua-roa mắc qua hai ròng rọc là:

l = MN + PQ + l 1 + l 2 = 2MN +  l 1 + l 2

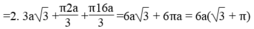
Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Đúng(0)
SG
Sách Giáo Khoa
9 tháng 5 2017
Cho một đa giác đều n cạnh có độ dài mỗi cạnh là a. Hãy tính bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp đa giác đều đó ? Hướng dẫn : Tính \(\widehat{COB}\) rồi tính \(\sin\widehat{COB}\) và \(tg\widehat{COB}\), từ đây tính được R và...
Đọc tiếp

Cho một đa giác đều n cạnh có độ dài mỗi cạnh là a. Hãy tính bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp đa giác đều đó ?

Hướng dẫn : Tính \(\widehat{COB}\) rồi tính \(\sin\widehat{COB}\) và \(tg\widehat{COB}\), từ đây tính được R và r
#Hỏi cộng đồng OLM #Toán lớp 9
1
NT
Nguyen Thuy Hoa
8 tháng 6 2017

Đường tròn nội tiếp. Đường tròn ngoại tiếp

Đúng(0)
SG
Sách Giáo Khoa
27 tháng 4 2017

Điểm hạ cánh của một máy bay trực thăng ở giữa hai người quan sát A và B. Biết khoảng cách giữa hai người này là 300m, góc "nâng" để nhìn thấy máy bay tại ví trí A là \(40^0\) và tại vị trí B là \(30^0\) (h.34). hãy tìm độ cao của máy bay ?
#Hỏi cộng đồng OLM #Toán lớp 9
1
PT
Phạm Trang
26 tháng 7 2017

Gọi C là vị trí của máy bay.

Kẻ CH⊥ABCH⊥AB

Trong tam giác vuông ACH, ta có:

AH=CH.cotgˆA(1)AH=CH.cot⁡gA^(1)

Trong tam giác vuông BCH, ta có:

BH=CH.cotgˆB(2)BH=CH.cot⁡gB^(2)

Từ (1) và (2) suy ra:

(AH+BH)=CH.cotgˆA+CH.cotgˆB(AH+BH)=CH.cot⁡gA^+CH.cot⁡gB^

Suy ra:

CH=ABcotgˆA+cotgˆB=ABcotg40∘+cotg30∘≈102,606(cm)



Đúng(0)
SG
Sách Giáo Khoa
27 tháng 4 2017

Cho hình 76, trong đó hai đường tròn (O) và (O') tiếp xúc nhau tại A. Chứng minh rằng các tiếp tuyến Bx và Cy song song với nhau.
#Hỏi cộng đồng OLM #Toán lớp 9
1
NT
Nguyen Thuy Hoa
23 tháng 6 2017

Đường tròn

Đúng(0)
SG
Sách Giáo Khoa
27 tháng 4 2017

Cho hai đường tròn (O) và (O') cắt nhau tại A và B như hình 77. Biết OA = 15cm, O'A = 13 cm, AB = 24cm. Tính độ dài OO' ?
#Hỏi cộng đồng OLM #Toán lớp 9
1
NT
Nguyen Thuy Hoa
23 tháng 6 2017

Đường tròn

Đúng(0)
SG
Sách Giáo Khoa
27 tháng 4 2017

Cho hai đường tròn (O), (O') tiếp xúc nhau tại A như trên hình 78. Chứng minh rằng các bán kính OBm O'C song song với nhau ?

 
#Hỏi cộng đồng OLM #Toán lớp 9
1
NL
Nguyễn Lê Phước Thịnh
16 tháng 5 2022

Ta có: ΔO'AC cân tại O'

nên \(\widehat{CO'A}=180^0-2\cdot\widehat{A}\)(1)

Ta có: ΔOBA cân tại O

nên \(\widehat{BOA}=180^0-2\cdot\widehat{A}\)(2)

Từ (1) và (2) suy ra \(\widehat{CO'A}=\widehat{BOA}\)

mà hai góc này là hai góc ở vị trí đồng vị

nên O'C//OB

Đúng(0)
SG
Sách Giáo Khoa
27 tháng 4 2017

Cho hai đường tròn (O; R) và (O'; r). Điền vào chỗ trống của bảng sau :
#Hỏi cộng đồng OLM #Toán lớp 9
1
NL
Nguyễn Lê Phước Thịnh
16 tháng 5 2022

undefined

Đúng(0)
SG
Sách Giáo Khoa
13 tháng 4 2017

Hình viên phân là phần hình tròn giới hạn bởi một cung và dây căng cung ấy. Hãy tính diện tích hình viên phân AmB, biết góc ở tâm \(\widehat{AOB}=60^o\) và bán kính đường tròn là 5,1 cm.
#Hỏi cộng đồng OLM #Toán lớp 9
1
TT
Thien Tu Borum
13 tháng 4 2017

Hướng dẫn giải:

∆OAB là tam giác đều có cạnh bằng R = 5,1cm. Áp dụng công thức tính diện tích tam giác đều cạnh a là a2√44 ta có

S∆OBC = SΔOBC=R2√34 (1)

Diện tích hình quạt tròn AOB là:

π.R2.6003600=πR26 (2)

Từ (1) và (2) suy ra diện tích hình viên phân là:

πR26−R2√34=R2(π6−√34)

Thay R = 5,1 ta có Sviên phân ≈ 2,4 (cm2)

Đúng(0)
SG
Sách Giáo Khoa
26 tháng 4 2017

Hai vệ tinh đang bay ở vị trí A và B cùng cách mặt đất 230km có nhìn thấy nhau hay không nếu khoảng cách giữa chúng theo đường thẳng là 2200 km ? Biết rằng bán kính R của trái đất gần bằng 6370 km và hai vệ tinh nhìn thấy nhau nếu OH > R (h.6)
#Hỏi cộng đồng OLM #Toán lớp 9
2
NT
Nguyen Thuy Hoa
31 tháng 5 2017

Hệ thức lượng trong tam giác vuông

Đúng(0)
NH
Nguyễn Huyền Trâm
4 tháng 9 2019

Vì hai vệ tinh cùng cách mặt đất 230 km nên tam giác AOB cân tại O.

Ta có: OA = R + 230

= 6370 + 230 = 6600 (km)

Trong tam giác AOB ta có: OH ⊥ AB

\(\Rightarrow\): HA = HB = AB/2 = 2200/2 = 1100 (km)

Áp dụng định lí Pi-ta-go vào tam giác vuông AHO, ta có:

OA2 = AH2 + OH2

\(\Rightarrow\): OH2 = OA2 – AH2

\(\Rightarrow\) :OH = 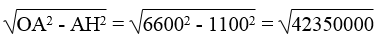Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9 ≈ 6508 (km)

Vì OH > R nên hai vệ tinh nhìn thấy nhau.

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP