Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi l là chiều dài của dây treo. Khi chưa trao đổi điện tích với nhau thì khoảng cách giữa hai quả cầu là l. Lực đẩy giữa hai quả cầu là : F 1 = k q 1 q 2 / l 2
Tương tự như ở Hình 1.1 G, ta có : tan 30 ° = (1) với P là trọng lượng quả cầu.
Khi cho hai quả cầu trao đổi điện tích với nhau thì mỗi quả cầu mang điện tích q 1 + q 2 /2. Chúng vẫn đẩy nhau và khoảng cách giữa chúng bây giờ là l 2
Lực đẩy giữa chúng bây giờ là :
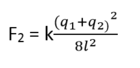
Tương tự như trên, ta có:
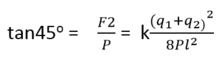 (2)
(2)
Từ (1) và (2) suy ra: 8 3 q 1 q 2 = q 1 + q 2 2
Chia hai vế cho q 2 2 ta có:
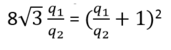
Đặt q 1 / q 2 = x ta có phương trình:
x 2 + (2- 8 3 )x + 1 = 0
hay x 2 - 11,86x + 1 = 0
Các nghiệm của phương trình này là x 1 = 11,77 và x 2 = 0,085
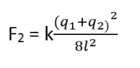

Đáp án A
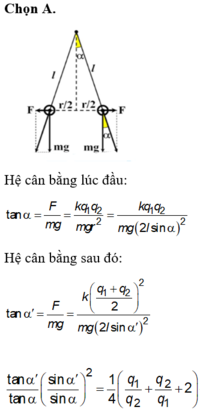
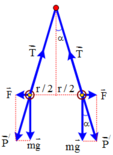
Hệ cân bằng lúc đầu:
tan α = F m g = k q 1 q 2 m g r 2 = k q 1 q 2 m g 2 ℓ sin α 2
Hệ cân bằng sau đó:
tan α ' = F m g = k q 1 + q 2 2 2 m g 2 ℓ sin α ' 2
tan α ' tan α sin α ' sin α = 1 2 q 1 q 2 + q 2 q 1 + 2 → q 1 q 2 = 7 , 5 q 1 q 2 = 0 , 13



Sau khi cho hai quả cầu tiếp xúc với nhau thì mỗi quả cầu sẽ mang điện tích:
\(q'=\dfrac{q+0}{2}=\dfrac{q}{2}\)
Lực tương tác giữa hai quả cầu là lực điện: \(F=k.\dfrac{\left|q'\right|.\left|q'\right|}{r^2}=k.\dfrac{\left(\dfrac{q}{2}\right)^2}{2.sin\alpha.l}=k.\dfrac{\left(\dfrac{q}{2}\right)^2}{2.sin30^0}=k\left(\dfrac{q}{2}\right)^2\)
Xét một trong hai quả cầu (giả sử quả cầu nằm bên trái), ta có:
\(tan\alpha=\dfrac{F}{P}=\dfrac{k\left(\dfrac{q}{2}\right)^2}{mg}\)
\(\Rightarrow\left|q\right|=2\sqrt{\dfrac{tan\alpha.mg}{k}}=2\sqrt{\dfrac{tan30^0.5.10^{-3}.10}{9.10^9}}=3,58.10^{-6}C\)

a) Chiều lên phương của sợi dây:
\(T\cos a=P=mg\)
\(T\sin a=F\left(F=kq_1.\frac{q_2}{r^2}\right)\)
Mà hai quả nhiểm điên như nhau.
\(\Rightarrow q_1=q_2=q\Rightarrow F=mg.\tan a\)
a là góc lệch sợi dây phương ngang.
Có: \(\sin a=\frac{r}{\left(2l\right)}\)
Vì a rất nhỏ \(\Rightarrow\sin a=\tan a=\frac{3}{50}\)
Thay vào ra \(F=3,6.10^{-4}\Rightarrow q=1,2.10^{-8}C\)
b) Lúc này: \(F=\frac{k.q^2}{e.r^2}\)
Với e là hằng số điện mới.
\(\Rightarrow F=\frac{mg.q^2}{er^2}=mg.\tan a=mg.\sin a=\frac{mg.r'}{2l'}\)
Thay vào tính được r' = 20 cm

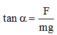
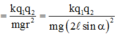
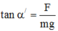
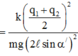
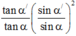
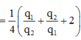

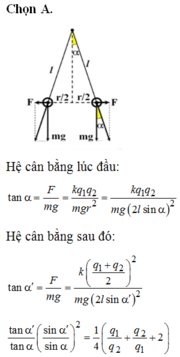


Đáp án A
Mình chưa hiểu cách giải lắm giúp mình được không ạ