Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Với giả thiết λ << L và L << d thì ta có thể coi bài toán giống như giao thoa sóng ánh sáng với:
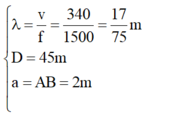
- Khoảng cách hai điểm gần nhau nhất mà nghe thấy âm nhỏ nhất tương ứng với 1 khoảng vân nên:
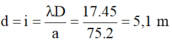

Gọi hình chiếu của điểm M trên AB là N, trung điểm của AB là O, đặt ON = x \(\Rightarrow\) \(AM=\sqrt{4+\left(4-x\right)^2}\)\(,BM=\sqrt{4+\left(4+x\right)^2}\)
\(\vartheta BM=\frac{2\pi BM}{\lambda}\)
\(\vartheta AM=\frac{2\pi AM}{\lambda}\)
\(\Rightarrow\frac{2\pi}{\lambda}\left(MB-MA\right)=\left(2k+1\right)\lambda\pi\)
Min khi k = 0 \(\Leftrightarrow\sqrt{4+\left(4+x\right)^2}-\sqrt{4+\left(4-x\right)^2}\)\(=1\Rightarrow x\approx0,56\left(cm\right)\)
chọn đáp án A

\(\lambda =\frac{v}{f}=\frac{50}{10}=5cm.\)
Điểm M ngược pha với điểm I khi: \(\triangle \phi=\phi_I-\phi_M = 2\pi \frac{d_1-d_{1}^{'}}{\lambda}=(2k+1)\pi \Rightarrow d_1-d_1^{'}=(2k+1)\frac{\lambda}{2}\)
Để điểm M gần I nhất thì hiệu d1 - d1' cũng phải nhỏ nhất khi đó k chỉ nhận giá trị nhỏ nhất là k = 0.
\(d_{1}-d_{1}^{'}=(2.0+1)\frac{5}{2}=2.5cm\Rightarrow d_1 = 7.5cm.\)
\(\Rightarrow MI= \sqrt {d_1^{2}-d_1^{'2}}\) = \(\sqrt{7.5^2-2.5^2}=\sqrt{50}cm\)

A B P d M d x d1 d2
\(d_1 - d_2 = \left( {\phi _m - \phi } \right)\dfrac{\lambda }{{2\pi }} = \left( {2k + 1} \right)\dfrac{{0.5\pi }}{{2\pi }} = \dfrac{k}{2} + 0.25 \)
Điểm M gần hất \(\Rightarrow k = 0 \Rightarrow d_1 - d_2 = 0.25 \)
\(\Rightarrow \sqrt {(\dfrac{d}{2} + x)^2 + 100^2 } - \sqrt {(\dfrac{d}{2} - x)^2 + 100^2 } = 0.25 \)
\(\Rightarrow \sqrt {(\dfrac{1}{2} + x)^2 + 100^2 } - \sqrt {(\dfrac{1}{2} - x)^2 + 100^2 } = 0.25 \)
\(\Rightarrow x = 25.82 m\)

Câu 1: Một sóng cơ hình sinh truyền theo chiều dương của trục OxOx. Khoảng cách giữa hai điểm gần nhau nhất trên OxOx mà phần tử môi trường ở đó dao động cùng pha nhau là
A. hai bước sóng.
B. một bước sóng.
C. một phần tư bước sóng.
D. một nửa bước sóng.
Câu 2: Đặc trưng nào sau đây là đặc trưng sinh lí của âm?
A. Tần số âm.
B. Độ cao của âm.
C. Cường độ âm.
D. Mức cường độ âm.
Câu 3: Một sợi dây đang có sóng dừng ổn định. Sóng truyền trên dây có bước sóng là 12 cm. Khoảng cách giữa hai nút liên tiếp là
A. 6 cm.
B. 3 cm.
C. 4 cm.
D. 12 cm.
Câu 4: Trong sóng cơ, công thức liên hệ giữa tốc độ truyền sóng vv, bước sóng λλ và chu kì TT của sóng là
A. λ=v2πTλ=v2πT.
B. λ=2πvT.λ=2πvT.
C. λ=vT.λ=vT.
D. λ=vT.λ=vT.
Câu 5: Giao thoa ở mặt nước được tạo bởi hai nguồn sóng kết hợp dao động điều hòa cùng pha theo phương thẳng đứng tại hai vị trí S1S1 và S2S2. Sóng truyền trên mặt nước có bước sóng 6 cm. Trên đoạn thẳng S1S2S1S2, hai điểm gần nhau nhất mà phần tử nước tại đó dao động với biên độ cực đại cách nhau
A. 12 cm.
B. 6 cm.
C. 3 cm.
D. 1,5 cm.
Câu 6: Một sợi dây dài 2 m với hai đầu cố định, đang có sóng dừng. Sóng truyền trên dây với tốc độ 20 m/s. Biết rằng tần số của sóng truyền trên dây có giá trị trong khoảng từ 11 Hz đến 19 Hzz. Tính cả hai đầu dây, số nút sóng trên dây là
A. 5.
B. 3.
C. 4.
D. 2.
Câu 1:
B. một bước sóng.
Câu 2:
B. Độ cao của âm.
.Câu 3:
B. 3 cm.
C. 4 cm.
D. 12 cm.
Câu 4:
C. λ=vT.λ=vT.
Câu 5:
C. 3 cm.
Câu 6:
C. 4.

Gọi H là đường chân cao hạ từ O đến MN
Giả sử OH = 1 → OM \(=\sqrt[4]{10};ON=\sqrt{10}\)
Do đó tính \(\widehat{MON}\approx1270,35^o\)
A đúng




+ Với giả thiết l << L và L << d thì ta có thể coi bài toán giống như giao thoa sóng ánh sáng với:
+ Khoảng cách hai điểm gần nhau nhất mà nghe thấy âm nhỏ nhất tương ứng với 1 khoảng vân nên:
Đáp án C