Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số cây 2 lớp trông được lần lượt là a và b .
\(\Rightarrow\begin{cases}\frac{a}{b}=\frac{4}{5}\\b-a=20\end{cases}\)\(\Rightarrow\begin{cases}\frac{a}{4}=\frac{b}{5}\\b-a=20\end{cases}\)
Áp dụng tc của dãy tỉ số bằng nhau ta có :
\(\frac{a}{4}=\frac{b}{5}=\frac{b-a}{5-4}=\frac{20}{1}=20\)
\(\Rightarrow\begin{cases}a=80\\b=100\end{cases}\)
Gọi x, y lần lượt là số cây trồng được của lớp 7A, 7B. Theo đề bài ta có: và y-x=20
Theo tính chất của dãy tỉ số bằng nhau ta có:
Do đó
Vậy số cây của lớp 7A là 80, của lớp 7B là 100

gọi số cây hai lớp 7a và 7b trồng được là a và b
Theo bài ra : \(\frac{a}{b}=0,8=\frac{8}{10}=\frac{4}{5}\) và b - a = 20
\(\frac{a}{b}=\frac{4}{5}\Rightarrow\frac{a}{4}=\frac{b}{5}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\frac{a}{4}=\frac{b}{5}=\frac{b-a}{5-4}=20\)
\(\Rightarrow a=4.20=80;b=20.5=100\)
Vậy số cây trồng được của hai lớp 7a và 7b lần lượt là 80 cây và 100 cây
Nguyễn Mai Linh
\(0,8=\frac{8}{10}=\frac{4}{5}\)
Gọi x , y là lần lượt số cây trồng của lớp 7A và 7B .
Theo đề bài ta có :
\(\frac{4}{5}=\frac{x}{y}\)
\(\Rightarrow\frac{x}{4}=\frac{y}{5}\)và \(y-x=20\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{4}=\frac{y}{5}=\frac{y-x}{5-4}=\frac{20}{1}=20\)
Suy ra :
\(\frac{x}{4}=20\Rightarrow x=4\cdot20=80\)
\(\frac{y}{5}=20\Rightarrow y=5\cdot20=100\)
Vậy số cây lớp 7A trồng được 80 cây và lớp 7B trồng được 100 cây .

Gọi x, y lần lượt là số cây trồng được của lớp 7A, 7B. Theo đề bài ta có:
xy=0,8=810=45=>x4=y5xy=0,8=810=45=>x4=y5 và y – x = 20
Theo tính chất của dãy tỉ số bằng nhau ta có:
x4=y5=y−x5−4=201=20x4=y5=y−x5−4=201=20
Do đó: x4=20=>x=20.4=80x4=20=>x=20.4=80
y5=20=>y=20.5=100y5=20=>y=20.5=100
Vậy số cây của lớp 7A là 80, của lớp 7B là 100
gọi x , y lần lượt là số cây trồng được của lớp 7A ,7B . theo đề bài ta có :
xy = 0,8 =810=45=>x4=y5xy=0,8=810=45=>x4=y5 và y-x =20
theo tính chất của dãy tỉ số bằng nhau ta có
x4=y5=y-x5-4=201=20x4=y5=y-x5-4=201=20
do đó : x4 = 20 => x = 20.4 = 80 x 4 =20=>20.4=80
y5=20=>y=20.5=100y5=20=>y=20.5=100
vậy số cây của lớp 7A là 80 , của lớp 7B là 100

Gọi số cây mỗi lớp đã trồng là lớp 7A và 7B lần lượt là e[cây] và f[cây]
Vì tỉ số giữa cây trồng được của lớp 7A và 7B là 0,8 nên ta có :
\(\frac{e}{f}=\frac{4}{5}\Leftrightarrow\frac{e}{4}=\frac{f}{5}\)
Mà lớp 7B trồng nhiều hơn lớp 7A là 20 cây nên ta lại có :
f - e = 20
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{e}{4}=\frac{f}{5}\Leftrightarrow\frac{f-e}{5-4}=\frac{20}{1}=20\)
Đến đây là ez rồi
Bài giải : Đổi : 0,8 = 4/5
Gọi số cây lớp 7A; 7B trồng được lần lượt là a,b (Đk: cây; a,b \(\in\)N*)
Theo bài ra, ta có: \(\frac{a}{4}=\frac{b}{5}\) và b - a = 20
Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{4}=\frac{b}{5}=\frac{b-a}{5-4}=\frac{20}{1}=20\)
=> \(\hept{\begin{cases}\frac{a}{4}=20\\\frac{b}{5}=20\end{cases}}\)=> \(\hept{\begin{cases}a=20.4=80\\b=20.5=100\end{cases}}\)
Vậy số cây của lớp 7A và 7B trồng được lần lượt là 80 cây, 100 cây

0,8 = 8/10 = 4/5
Gọi x,y lần lượt là số cây trông lớp 7A và 7B
Theo đề bài, ta có:
4/5 = x/y
=> x/4 = y/5 và y - x = 20
Áp dụng tìh chất dãy tỉ số bằng nhau ta có :
x/4 = y/5 = y-x/5-4 = 20/1 = 20
Suy ra : x/4 = 20 -> x = 4.20 = 80
y/5 = 20 -> y = 5.20 = 100
Vậy lớp 7A trồng được 80 cây
lớp 7B trồng được 100 cây
Gọi x, y lần lượt là số cây trồng được của lớp 7A, 7B. Theo đề bài ta có:
và y - x = 20
Theo tính chất của dãy tỉ số bằng nhau ta có:
Do đó:
Vậy số cây của lớp 7A là 80, của lớp 7B là 100

Gọi số cây hai lớp 7A, 7B trồng lần lượt là x, y ( cây) (điều kiện x, y là số nguyên dương)
theo bài ra tỉ số giữa số cây trồng được lớp 7A và lớp 7B là 0,8 nên x:y = 0,8
--> x/y = 8/10 = 4/5 --> x =4/5 y (1)
lớp 7B trồng nhiều hơn lớp 7A 20 cây nên ta có y- x =20 (2)
thay (1) vào (2) ta có: y - 4/5 y = 20 --> 1/5 y = 20
--> y = 100 (cây) --> x= 4/5*100 = 80 (Cây)
Vậy hai lớp 7A, 7B trồng được 80 và 100 cây
0,8 = 8/10 = 4/5
Gọi x,y lần lượt là số cây trông lớp 7A và 7B
Theo đề bài, ta có:
4/5 = x/y => x/4 = y/5
và y - x = 20
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
x/4 = y/5 = y-x/5-4 = 20/1 = 20
=> x/4 = 20 -> x = 4.20 = 80
y/5 = 20 -> y = 5.20 = 100
Vậy lớp 7A trồng được 80 cây
lớp 7B trồng được 100 cây
nguồn:Câu hỏi của Ngô Phúc Hưng - Toán lớp 7 - Học toán với OnlineMath

Gọi số cây lớp 7A trồng được là `a.`
Gọi số cây lớp 7B trồng được là `b.`
Điều kiện: `a, b in NN, b > 20`, đơn vị: cây.
Từ bài toán, ta có `{(a/b= 0,8=4/5), (b-a=20:}`
`<=> 5a = 4b` và `b - a =20`.
`<=> 4b - 4a = 80`.
`<=> 5a - 4a = 80`.
`<=> a = 80`.
`=> b = 80 : 4 xx 5 = 100`
Vậy lớp 7A, 7B trồng được lần lượt 80, 100 cây.

Bài làm:
Gọi số cây trồng được của lớp 7A, 7B lần lượt là x (cây); y (cây).
Tỉ số giữa số cây trồng được của lớp 7A và lớp 7B là 0,8 nghĩa là x : y =0,8 hay 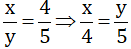
Lớp 7B trồng nhiều hơn lớp 7A là 20 cây nghĩa là y – x = 20.
Theo tính chất dãy tỉ số bằng nhau
Vậy Lớp 7A trồng được 80 cây
Lớp 7B trồng được 100 cây
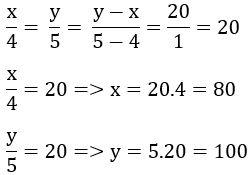
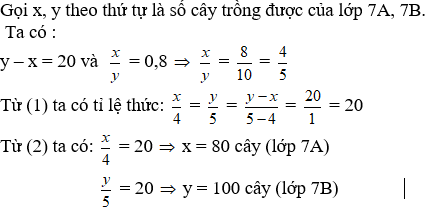
Câu hỏi của Phạm Thị Quỳnh Anh - Toán lớp 7 - Học toán với OnlineMath
7A: 20 : (10-8) x 8 = 80 cây
7B: 80 + 20 = 100 cây