Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số cây trồng 3 lớp lần lượt là \(a,b,c\left(a,b,c>0\right)\)
Áp dụng TCDTSBN:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{\left(a+c\right)-b}{\left(3+5\right)-4}=\dfrac{20}{4}=5\)
\(\Rightarrow\left\{{}\begin{matrix}a=3\cdot5=15\left(cay\right)\\b=4\cdot5=20\left(cay\right)\\c=5\cdot5=25\left(cay\right)\end{matrix}\right.\)

Gọi số cây lớp 7A,7B,7C trồng được lần lượt là a(cây), b(cây),c(cây)
(Điều kiện: \(a\in Z^+;b\in Z^+;c\in Z^+\))
Số cây của lớp 7A,7B,7C lần lượt tỉ lệ với 6;4;5 nên ta có:
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{5}\)
Tổng số cây trồng được của 2 lớp 7A,7B nhiều hơn của lớp 7C là 50 cây nên ta có: a+b-c=50
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b-c}{6+4-5}=\dfrac{50}{5}=10\)
=>a=60;b=40;c=50
Vậy: Lớp 7A trồng được 60 cây
Lớp 7B trồng được 40 cây
Lớp 7C trồng được 50 cây

Giải:
Gọi số cây lớp 7A và lớp 7B lần lượt là: a,b ( a,b > 0 )
Theo bài ra ta có:
\(a=0,8.b\Rightarrow a=\frac{4}{5}.b\Rightarrow\frac{a}{4}=\frac{b}{5}\) và b - a = 20
Theo tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{4}=\frac{b}{5}=\frac{b-a}{5-5}=\frac{20}{1}=20\)
+) \(\frac{a}{4}=20\Rightarrow a=80\)
+) \(\frac{b}{5}=20\Rightarrow b=100\)
Vậy lớp 7A trồng được 80 cây
lớp 7B trồng được 100 cây
Gọi x, y lần lượt là số cây trồng được của lớp 7A, 7B. Theo đề bài ta có:
và y - x = 20
Theo tính chất của dãy tỉ số bằng nhau ta có:
Do đó:
Vậy số cây của lớp 7A là 80, của lớp 7B là 100

\(0.8=\frac{8}{10}=\frac{4}{5}\)
Gọi x,y là số cây trồng lớp 7A và 7B
Theo đề bài ta có:
\(\frac{4}{5}=\frac{x}{y}\)
=>\(\frac{x}{4}=\frac{y}{5}\) và y-x=20
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(^{\frac{x}{4}=\frac{y}{5}=\frac{y-x}{5-4}\frac{20}{1}=20}\)
- \(\frac{x}{4}=4.20=80\)
- \(\frac{y}{5}=5.20=100\)
Vậy lớp 7A trồng được 80 cây.
lớp 7B trồng được 100 cây
Ủng hộ mk nha bạn ^...^
0,8 = 8/10 = 4/5
Gọi x,y lần lượt là số cây trông lớp 7A và 7B
Theo đề bài, ta có:
4/5 = x/y
=> x/4 = y/5 và y - x = 20
Áp dụng tìh chất dãy tỉ số bằng nhau ta có :
x/4 = y/5 = y-x/5-4 = 20/1 = 20
Suy ra : x/4 = 20 -> x = 4.20 = 80
y/5 = 20 -> y = 5.20 = 100
Vậy lớp 7A trồng được 80 cây
lớp 7B trồng được 100 cây

Gọi số cây lớp 7A trồng được là `a.`
Gọi số cây lớp 7B trồng được là `b.`
Điều kiện: `a, b in NN, b > 20`, đơn vị: cây.
Từ bài toán, ta có `{(a/b= 0,8=4/5), (b-a=20:}`
`<=> 5a = 4b` và `b - a =20`.
`<=> 4b - 4a = 80`.
`<=> 5a - 4a = 80`.
`<=> a = 80`.
`=> b = 80 : 4 xx 5 = 100`
Vậy lớp 7A, 7B trồng được lần lượt 80, 100 cây.

1,Ta có 7A/7B=0,8=4/5
Gọi số cây h/s lớp 7A trồng được là x (học sinh), (x>0)
Số cây h/s lớp 7B trồng được là x+20
Vì tỉ số trồng cây của lớp 7A và lớp 7B là 0,8 nên ta có phương trình:
x/ x+20 = 4/5
5x=4(x+20)
5x= 4x+80
5x-4x=80
x=80
Với x=80 thoả mãn đk trên.
Vậy số cây lớp 7A trồng được là 80 cây
Số cây lớp 7B trồng được là 80+20=100 cây
2,
goi a, b lan luot la 7a va 7b
x/y=8/9=x/8=y/9 va y-x=5
Ap dung tinh chat day ti so bang nhau ta co :
x/8=y/9=y-x/9-8=5/1=5
suy ra : x/8=5=>x=5.8=40
y/9=5=>y=9.5=45

Bài làm:
Gọi số cây trồng được của lớp 7A, 7B lần lượt là x (cây); y (cây).
Tỉ số giữa số cây trồng được của lớp 7A và lớp 7B là 0,8 nghĩa là x : y =0,8 hay 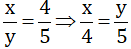
Lớp 7B trồng nhiều hơn lớp 7A là 20 cây nghĩa là y – x = 20.
Theo tính chất dãy tỉ số bằng nhau
Vậy Lớp 7A trồng được 80 cây
Lớp 7B trồng được 100 cây

Giải
Đổi 0,8 =\(\frac{8}{10}\)
Hiệu số phần bằng nhau là :
10 - 8 = 2 ( phần )
Số cây lớp 7A đã trồng là :
20 : 2 x 8 = 80 ( cây )
Số cây lớp 7B đã trồng là :
20 + 80 = 100 ( cây )
Đáp số : 7A : 80 cây
7B : 100 cây
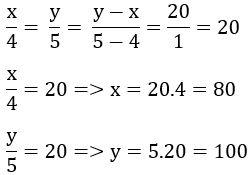
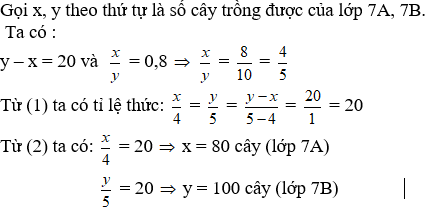
7A: 60 cây
7B: 40 cây
Cài này phải giải chi tiết ra