Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm

c.
\(\dfrac{1}{T^2}=\dfrac{1}{T_{1^{ }}^2}+\dfrac{1}{T_2^2}\)
=> T=0,24s

Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)

Bài này có vẻ lẻ quá bạn.
\(W_t=4W_đ\Rightarrow W_đ=\dfrac{W_t}{4}\)
Cơ năng: \(W=W_đ+W_t=W_t+\dfrac{W_t}{4}=\dfrac{5}{4}W_t\)
\(\Rightarrow \dfrac{1}{2}kA^2=\dfrac{5}{4}.\dfrac{1}{2}kx^2\)
\(\Rightarrow x = \pm\dfrac{2}{\sqrt 5}A\)
M N O α α
Thời gian nhỏ nhất ứng với véc tơ quay từ M đến N.
\(\cos\alpha=\dfrac{2}{\sqrt 5}\)\(\Rightarrow \alpha =26,6^0\)
Thời gian nhỏ nhất là: \(\Delta t=\dfrac{26,6\times 2}{360}.T=\dfrac{26,6\times 2}{360}.\dfrac{2\pi}{20}=0.046s\)

\(\Delta l=\frac{g}{\omega^2}=0,25m\)
\(t=0\Rightarrow x=5\sqrt{3}cm\Rightarrow l=l_0+\Delta l+x=158,66cm\)
Vậy không phương án đúng

\(\lambda = v/f = 0.8/100 = 0.008m = 0.8cm.\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{0}{\lambda}-\frac{0}{2\pi})| = |2a| = 2a.\)
\(u_M = A_M\cos(2\pi ft - \pi\frac{d_2+d_1}{\lambda}+\frac{\varphi_1+\varphi_2}{2})\\= A_M\cos(200\pi t - \pi\frac{8+8}{0.8}+\frac{0}{2})= 2a\cos(200\pi t - \pi\frac{8+8}{0.8})= 2a\cos(200\pi t-20\pi)=2a\cos(200\pi t)\)

Khi qua VTCB, tốc độ của con lắc đạt cực đại là:
\(v_{max}=\omega A =\sqrt{\dfrac{k}{m}}.A\)
\(\Rightarrow m = \dfrac{kA^2}{v_{max}^2}=\dfrac{a}{v_{max}^2}\) (vì \(kA^2=const\))
Theo đề bài ta có: \(m_3=9m_1+4m_2\)
\(\Rightarrow \dfrac{a}{v_3^2}=\dfrac{9a}{v_1^2}+\dfrac{4a}{v_2^2}\)
\(\Rightarrow \dfrac{1}{v_3^2}=\dfrac{9}{v_1^2}+\dfrac{4}{v_2^2}\)
\(\Rightarrow \dfrac{1}{v_3^2}=\dfrac{9}{20^2}+\dfrac{4}{10^2}\)
\(\Rightarrow v_3=4m/s\)
Chọn đáp án B.

Áp dụng công thức tính năng lượng dao động của con lắc đơn ta có:
\(W_1 = \dfrac{1}{2}.m_1.g.\ell_1. \alpha_1 ^{2}\) và \(W_2 = \dfrac{1}{2}.m_2.g.\ell_2. \alpha_2 ^{2}\)
Theo giả thiết hai con lắc đơn có cùng năng lượng
\(\Rightarrow \dfrac{1}{2}.m_1.g.\ell_1. \alpha_1 ^{2}=\dfrac{1}{2}.m_2.g.\ell_2. \alpha_2 ^{2}\)
Do khối lượng hai con lắc bằng nhau nên:
\(\ell_1.\alpha_1 ^{2} = \ell_2. \alpha_2 ^{2}\)
\(\Rightarrow \alpha_2 = \alpha_1 .\sqrt{l1/l2}\).
Thay số ta tìm được: \(\alpha_2 = 5,625^0\)
Chọn B
+ Có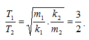
Thay m1 = 4m2 =>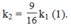
+ Mắc hai lò xo k1, k2 thành một lò xo dài gấp đôi, đầu trên cố định, đầu dưới treo vật m2.
=> Độ cứng của lò xo mới là: