Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài toán này rất hay, cô sẽ giải thích cho em nhé :)
Xét tam giác FAH và tam giác FAI có:
AI = AH ( Vì cùng bằng AE).
AF chung.
Ta cần chứng minh góc FAI = góc HAF.
Gọi giao điểm AB với IE là M, của AC với EH là N.
Khi đó ta có góc FAI = góc IAM + MAE + EAF = góc EAF + 2 góc FAN. (1)
góc HAF = góc FAN + NAH, mà góc NAH = góc EAF + góc FAN nên góc HAF = góc EAF + 2 góc FAN. (2)
Từ (1), (2) suy ra góc FAI = góc HAF.
Vậy tam giác FAI bằng tam goác FAH (c-g-c).
và đây là hình,nó có vẻ hơi xấu và sai 1 số chỗ nhỏ bạn thông cảm
I A H C K F E B

Ta có:
* SADB=SACB=SDAC=SDBC ( cùng bằng \(\dfrac{1}{2}.S_{hbh}\) )
* SOAD=SOCB=SODC=SOBA (cùng bằng \(\dfrac{1}{4}.S_{hbh}\))

A B C H E F G
a) Ta có: AB = AE + EB ; AC = AF+ FC
mà AB = AC (gt); EB = CF (gt)
=> AE = AF => t/giác AEF cân tại A
=> \(\widehat{AEF}=\widehat{AFE}=\frac{180^0-\widehat{A}}{2}\) (1)
T/giác ABC cân tại A => \(\widehat{B}=\widehat{C}=\frac{180^0-\widehat{A}}{2}\)(2)
Từ (1) và (2) => \(\widehat{AEF}=\widehat{B}\) mà 2 góc này ở vị trí đồng vị
=> EF // BC => tứ giác EFCB là hình thang có \(\widehat{B}=\widehat{C}\)
=> BEFC là hình thang cân
b) Ta có: \(\widehat{AFE\:}=\widehat{AEF}=\frac{180^0-\widehat{A}}{2}=\frac{180^0-40^0}{2}=70^0\)
\(\widehat{AFE\:}+\widehat{EFC\:}=180^0\) (kề bù) => \(\widehat{EFC\:}=180^0-\widehat{AFE\:}=180^0-70^0=110^0\)
c) Kẻ FG vuông góc với BC
Ta có: EF // BC (cmt)
EH \(\perp\)BC (gt)
=> HE \(\perp\)EF
Xét tứ giác EFGH có \(\widehat{HEF}=\widehat{EHG}=\widehat{HGF}=90^0\)
=> EFGH là HCN => EH = FG = 5 cm
St/giác BFC = 5.10/2 = 25 (cm2)

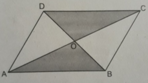
Xem hình bs.52.
- Các tam giác ADB, ACB, DAC, DBC có diện tích bằng nhau vì cùng bằng nửa diện tích hình bình hành đã cho.
- Các tam giác OAD, OCB, ODC, OBA có diện tích bằng nhau vì cùng bằng một phần tư diện tích hình bình hành đã cho.

A)
Ta có : K đối xứng với M qua I ( gt ) => IM = IK (1)
I là trung điểm của AC (gt) => IA=IC (2)
Mà Tam giác ABC cân tại A (gt) nên AM là đường cao của tam giác ABC => AM vuông góc với BC nên góc M = 900
Hình bình hành AMCK có góc M = 900 nên AMCK là hình chữ nhật
B)
Theo a : tứ giác AMCK là hình chữ nhật nên AK=MC và AK // MC => AK // BM
Mà AM là đường trung tuyến của tam giác ABC (gt) nên BM = MC
=> AK = BM , AK // BM
=> Tứ giác AKMB là hình bình hành
C)
Ta có : AM = ML (gt)
BM = MC (Vì AM là đường trung tuyến của tam giác ABC )
Nên Tứ giác ABLC là hình bình hành
Mà AB=AC ( vì tứ giác ABC cân tại A)
=> TỨ giác ABLC là hình thoi

\(\frac{ljkl\sqrt{ljkljkl\widehat{lkljkljkl}}}{jkljkl\frac{jklj}{kljk}ljkljkl\orbr{\begin{cases}ljklkjlj\\ljklklj\end{cases}}klj}ljk\)ljkljkljkl jljk jkljlk
jljk jkljlk