Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Độ lệch pha giữa hai dao động là ∆φ = 0,75π – 0,5π = 0,25π rad.

Trong dao động cưỡng bức, biên độ đạt cực đại khi hiện tượng cộng hưởng xảy ra.
Suy ra \(1,25 < f_0 < 1,3\)
→ \(2,5\pi < \omega < 2,6\pi\)
Có \(k = m \omega ^2\) → \(13,3 < k < 14,4\)
→ \(k \approx 13,64 N/m\).

2 trường hợp cho cùng cường độ dòng nên kháng trong 2 trường hợp như nhau và ta đã biết quận không thuần cảm
\(\frac{1}{C\omega_1}-L\omega_1=L\omega_2-\frac{1}{C\omega_1}\)
\(LC\omega_1\omega_2=1\)
\(Z_{C_1}=\frac{1}{C\omega_1}=L\omega_2=Z_{L_2}=62,5\Omega\)
\(Z_{L_1}=40\Omega\)
\(Z=\frac{U}{I}\approx54,83\Omega\)
\(r=50\Omega\)
Cường độ dòng hiệu dụng cực đại sẽ là
\(I'=\frac{U}{r}=4A\)

Ta có : ADCT : \(I_0=U_0\sqrt{\frac{C}{L}}\) ( Từ công thức tính năng lượng điện từ trong mạch \(W=W_{Cmax}=W_{Lmax}\)
Nghĩa là :\(\frac{L.\left(I_0\right)^2}{2}=\frac{C.\left(U_0\right)^2}{2}\))
\(\Rightarrow I_0=5.\sqrt{\frac{8.10^{-9}}{2.10^{-4}}}=\text{0.0316227766}\left(A\right)\)\(\Rightarrow I=\frac{I_0}{\sqrt{2}}=\text{0.022360677977}\left(A\right)\)
Mà \(P=r.I^2\Rightarrow r=\frac{6.10^{-3}}{5.10^{-4}}=12\left(\Omega\right)\Rightarrow D\)

\(U_C=I.Z_C=\dfrac{U.Z_C}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}.\omega C}=\dfrac{U}{\sqrt{\omega^2.C^2.R^2+(\omega^2.LC-1)^2}}\)
Suy ra khi \(\omega=0\) thì \(U_C=U\) \(\Rightarrow (1)\) là \(U_C\)
\(U_L=I.Z_L=\dfrac{U.Z_L}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U.\omega L}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}}=\dfrac{U.L}{\sqrt{\dfrac{R^2}{\omega^2}+(L-\dfrac{1}{\omega^2 C})^2}}\)(chia cả tử và mẫu cho \(\omega\))
Suy ra khi \(\omega\rightarrow \infty\) thì \(U_L\rightarrow U\) \(\Rightarrow (3) \) là \(U_L\)
Vậy chọn \(U_C,U_R,U_L\)

Khi trong mạch xảy ra cộng hưởng thì ω = ${\omega _0} = \dfrac{1}{{\sqrt {LC} }}$.
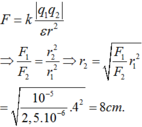


+ Ta có:
+ Vì hai điện tích trái dấu nên lực tương tác là lực hút => Chọn B