Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

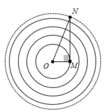
+ Các đường tròn nét liền biểu diễn các điểm cùng pha với nguồn. Điểm M nằm trên đỉnh sóng thứ 6 kể từ nguồn sóng O, N nằm trên điểm ngược pha gần nhất so với đỉnh sóng thứ 9 kể từ O, vậy
Từ hình vẽ ta thấy rằng, với điều kiện để trên MN có 4 điểm cùng pha với O thì rõ ràng MN lớn nhất khi MN vuông góc với OM
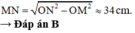

Chọn D
Bước sóng λ = v / f = 40 / 20 = 2 c m .
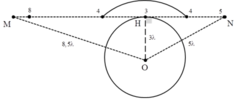
Các đường trong biểu diễn các điểm cùng pha với nguồn, N nằm trên đỉnh sóng thứ 5. M ngược pha nằm tại điểm gần đỉnh sóng thứ 8:
O N = 5 λ = 10 c m . O M = 8,5 λ = 17 c m .
Từ hình vẽ thấy để trên đoạn MN có 8 điểm cùng pha với nguồn thì MN phải tiếp tuyến với đỉnh sóng thứ 3 ( O H = 3 λ = 6 c m ) .
Ta có: M N = M H + H N = M O 2 − O H 2 + O N 2 − O H 2
⇒ M N = 17 2 − 6 2 + 10 2 − 6 2 ≈ 23,9 c m .

Đáp án B
Ta có λ = v f = 1 50 = 0 , 02 ( m ) = 2 c m
Hai điểm gần nhất dao động ngược pha cách nhau λ 2 = 1 c m

Trong quá trình truyền sóng, các điểm cách nhau một bước sóng sẽ dao động cùng pha, cách nhau một số lẻ lần nửa bước sóng sẽ dao động ngược pha.
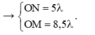
+ Giả sử rằng, tại thời điểm quan sát, O là một đỉnh sóng, khi đó quá trình lan truyền sóng được biểu diễn như hình vẽ.
+ Trên MN có 8 điểm dao động cùng pha với O → H phải là đỉnh sóng thứ 3 kể từ O (tính là thứ 0).

+ Khoảng cách giữa một điểm đứng yên (cực tiểu giao thoa) và một điểm dao động mạnh nhất (cực đại gia thoa) là 0,25λ = 3 → λ = 12 cm.
→ Vận tốc truyền sóng v = λf = 60 cm/s.
Chọn A

\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)

Đáp án: D
HD Giải: Hai điểm dao động ngược pha
![]()
=>  = 16(k + 0,5)
= 16(k + 0,5)
Vì 48Hz ![]() v
v ![]() 64Hz suy ra k = 3, f = 56Hz
64Hz suy ra k = 3, f = 56Hz


Hướng dẫn giải:
Tại P dao động mạnh nhất khi \(d_{2}-d_{1}=(k+\frac{\triangle \phi}{2\pi})\lambda.\)
Tại P dao động cực tiểu khi \(d_{2}-d_{1}=(2k+1+\frac{\triangle \phi}{\pi})\frac{\lambda}{2}.\)
\(\triangle \phi = \pi\)
\(\lambda = \frac{v}{f}=\frac{80}{20}=4cm.\) Tại N: \(d_{2N}-d_{1N}=61-33=28=9.2\) => N đứng yên.
Tại M: \(d_{2M}-d_{1M}=9.25-3.25=6=(1+\frac{1}{2}).4\)=> tại M dao động cực đại.