Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải thích: Đáp án B
Phương pháp: Sử dụng lí thuyết về năng lượng dao động của CLLX và dùng tam thức bậc 2 để nhận xét giá trị nhỏ nhất
Cách giải:
Biên độ dao động của các vật tính từ công thức 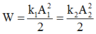
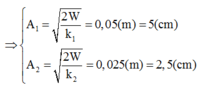
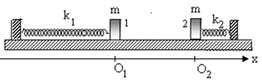
Khoảng cách lúc đầu giữa hai vật: O1O2 = 10 cm.
Chọn gốc thời gian là lúc bắt đầu dao động, chọn gốc tọa độ trùng với O1 thì phương trình dao động của các vật lần lượt là :![]() với ω là tần số góc của con lắc thứ nhất.
với ω là tần số góc của con lắc thứ nhất.
Khoảng cách giữa hai vật: ![]()
Ta thấy y là tam thức bậc 2 đối với cosωt và ymin khi cosωt = -0,5
Thay cosωt = 0,5 và biểu thức y ta tính được ymin = 6,25 cm.=> Chọn B

Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm

Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)

Đáp án A
Biên độ dao động của vật tính từ công thức:
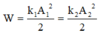
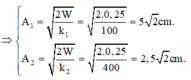
Khoảng cách lúc đầu giữa hai vật là: 10cm.
Chọn gốc thời gian là lúc bắt đầu dao động, chọn gốc tọa độ trùng với O1 thì phương trình dao động của các vật lần lượt là:
![]()
![]()
![]()
Khoảng cách giữa hai vật:
![]()
![]()
Ta thấy y là tam thức bậc hai đối với cos ω t và y m i n = cos ω t = - 0 , 5 Thay vào biểu thức ta tính được
![]()

Phương trình khoảng cách giữa 2 vật :
\(\Delta x=10\cos\left(\pi t\right)cm\)
Tại thời điểm 2 vật đi ngang qua nhau tức là cùng li độ.
Thời gian ngắn nhất chúng cách nhau thỏa mãn tại thời điểm t1, chúng cùng đi qua VTCB (tốc độ cực đại)
Thời gian \(\Delta x\)từ 0 đến 5cm xác định trên đường tròn
\(t=\frac{T}{12}=\frac{1}{6}s\)
Chọn A

Hai điểm cách gần nhau nhất là: \(\dfrac{\lambda}{2}=10\Rightarrow \lambda=20cm\)
M O1 O2 d1 d2
M dao động cực đại và cách O2 xa nhất khi M nằm ở vân ngoài cùng về phía O1.
Vị trí vân cực đại này là: \([\dfrac{196}{2.20}]=4\)
\(\Rightarrow d_2-d_1=4.\lambda=4.20=80cm\)
\(\Rightarrow d_2= d_1+80=196+80=276cm\)
Chọn D
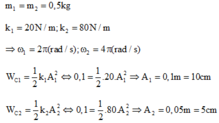
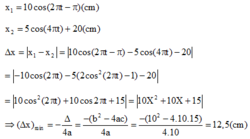
Giải thích: Đáp án B
Phương pháp: Sử dụng công thức tính cơ năng và tần sốgóc của con lắc lò xo
Khoảng cách hai vật trong quá trình dao động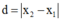
Cách giải:
Tần số góc của 2 vật: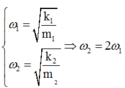
* Biên độ dao động của vật 1 là: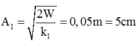
* Biên độ dao động của vật 1 là: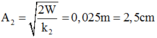
Đặt hệ trục tọa độ chung cho 2 vật như hình vẽ.
Thời điểm ban đầu vật 1 ở biên âm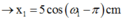
Thời điểm ban đầu vật 1 ở biên dương, chú ý tọa độ vị trí cân bằng O2 của vật thứ 2 là L
Khoảng cách 2 vật trong quá trình dao động là: