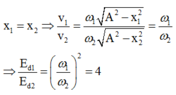Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
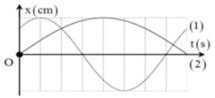
+ Từ đồ thị ta thấy hai dao động có cùng biên độ và
![]()
Tại vị trí hai dao động có cùng li độ
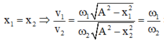
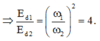

\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)

Hướng dẫn bạn:
- Lực kéo về: \(F=k.x=0,03\sqrt 2\pi\) (không biết có đúng như giả thiết của bạn không)
\(\Rightarrow x =\dfrac{0,03\sqrt 2\pi}{k}=\dfrac{0,03\sqrt 2\pi}{m.\omega^2}=\dfrac{0,03\sqrt 2\pi}{0,01.\omega^2}=\dfrac{3\sqrt 2\pi}{\omega^2}\)
- Áp dụng: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow 0,05^2=(\dfrac{3\sqrt 2\pi}{\omega^2})^2+\dfrac{(0,4\pi)^2}{\omega^2}\)
Bạn giải pt trên tìm \(\omega \) và suy ra chu kì \(T\) nhé.

Phương trình khoảng cách giữa 2 vật :
\(\Delta x=10\cos\left(\pi t\right)cm\)
Tại thời điểm 2 vật đi ngang qua nhau tức là cùng li độ.
Thời gian ngắn nhất chúng cách nhau thỏa mãn tại thời điểm t1, chúng cùng đi qua VTCB (tốc độ cực đại)
Thời gian \(\Delta x\)từ 0 đến 5cm xác định trên đường tròn
\(t=\frac{T}{12}=\frac{1}{6}s\)
Chọn A

Chọn đáp án B
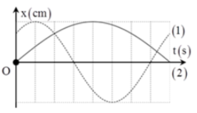
+ Từ đồ thị:
![]()
+ Lại có: 0 , 75 = T 1 2 ⇒ T 1 = 1 , 5 s
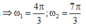
+ Ta lại có:
Tại: t = 0,75s ⇒ x = A c o s ( ω 2 t - π 2 )
⇒ x = A c o s ( 7 π 3 . 0 , 75 - π 2 ) = - A 2
= x 1 = - 5 c m ⇒ A = 5 2 c m
Suy ra: v m a x = ω 1 A = 4 3 . π 5 2 = 29 , 62 c m / s

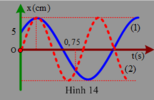
Giải thích: Đáp án D
+ Từ đồ thị ta thấy dao động có cùng biên độ và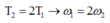
Tại vị trí hai dao động có cùng li độ