Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
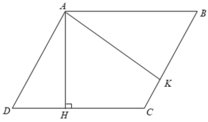
Xét hình bình bình ABCD có AB = CD = 8( cm ) và AD = BC = 6( cm )
Từ A kẻ các đường cao AH,AK.
Khi đó ta có:
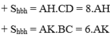
Mà một hình bình hành thì chỉ có một diện tích chung nên 8.AH = 6.AK
Nếu độ dài đường cao thứ nhất là AH = 5( cm ) thì:
8.5 = 6.AK ⇔ AK = (8.5)/6 = 20/3( cm ) là độ dài đường cao thứ hai.
Nếu độ dài đường cao thứ nhất là AK = 5( cm ) thì:
8.AH = 6.5 ⇔ AH = (6.5)/8 = 15/4( cm ) là độ dài đường cao thứ hai.
Vậy bài toán này có hai đáp số
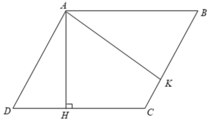
Xét hình bình bình ABCD có AB = CD = 8( cm ) và AD = BC = 6( cm )
Từ A kẻ các đường cao AH,AK.
Khi đó ta có:
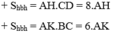
Mà một hình bình hành thì chỉ có một diện tích chung nên 8.AH = 6.AK
Nếu độ dài đường cao thứ nhất là AH = 5( cm ) thì:
8.5 = 6.AK ⇔ AK = (8.5)/6 = 20/3( cm ) là độ dài đường cao thứ hai.
Nếu độ dài đường cao thứ nhất là AK = 5( cm ) thì:
8.AH = 6.5 ⇔ AH = (6.5)/8 = 15/4( cm ) là độ dài đường cao thứ hai.
Vậy bài toán này có hai đáp số
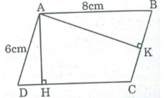
Giả sử hình bình hành ABCD cói AB = 8cm, AD = 6cm.
Kẻ AH ⊥ CD, AK ⊥ BC.Ta có 5 < 6, 5 < 8
Đường cao là cạnh góc vuông nhỏ hơn cạnh huyền thỏa mãn có hai trường hợp:
*Trường hợp 1: AK = 5cm
Ta có: S A B C D = AK.BC = 5.6 = 30 ( c m 2 )
S A B C D = AH.AD = 8.AH
Suy ra: 8.AH = 30 ⇒ AH = 30/8 = 15/4 (cm)
*Trường hợp 2: AH = 5cm
Ta có: S A B C D = AH.CD= 5.8 = 40 ( c m 2 )
S A B C D = AK.BC = 6.AH
Suy ra: 6.AK = 40 ⇒ AK = 40/6 = 20/3 (cm)
Vậy đường cao thứ hai có độ dài là 15/4 cm hoặc 20/3 cm
Bài toán có hai đáp số.
Nếu a là độ dài cạnh và h là đường cao tương ứng, b là cạnh kia và k là đường cao tương ứng thì ta có: a.h = b.k (vì cùng bằng diện tích hình bình hành).
Đối với bài toán đã cho, ta có 2 trường hợp sau:
Trường hơp 1: đường cao đã cho (5cm) ứng với cạnh 6cm. Khi đó đường cao thứ hai là: \(\dfrac{5.6}{8}=\dfrac{15}{4}\left(cm\right)\)
Trường hợp 2: đường cao 5cm ứng với cạnh 8cm, khi đó đường cao thứ hai là: \(\dfrac{5.8}{6}=\dfrac{20}{3}\left(cm\right)\)
Gọi x (cm) là độ dài đường cao thứ hai ứng với cạnh 8cm của hình bình hành (0 < x < 5)
Theo công thức tính diện tích hình bình hành ta có phương trình:
6.5 = 8.x ⇔ 8x =30 ⇔ x = 3,75 (tmđk)
Vậy độ dài đường cao thứ hai là 3,75cm
Gọi đường cao còn lại là h.
Theo quan hệ giữa đường xiên và hình chiếu thì ta có chiều cao của hình bình hành luôn nhỏ hơn cạnh không tương ứng với nó.
⇒ Đường cao có độ dài bằng 5cm ứng với cạnh 4cm
⇒ SABCD = 4.5 = 20
Mà SABCD = h.6
⇒ h.6 = 20 ⇒ h = 20 : 6 = 3,33 (cm).
DBDC, viết các cặp góc tương ứng bằng nhau của hai tam giác đã cho. 
có AB = 3cm, AC = 4,5cm, BC = 6cm. 
có DE= 12cm, EF=9cm, DF = 6cm. Chứng minh 
. 
AC). Tính AN? 
nhọn. Trên cạnh Ox, đặt các đoạn thẳng OA = 6cm, OB = 18cm. Trên cạnh Oy, đặt các đoạn thẳng OC = 9cm, OD = 12cm.Chứng minh hai tam giác OAD và OCB đồng dạng. 
có 
và 
có MN = 6cm; MP = 8cm; 
đồng dạng với 
Câu 11:
Xét ΔABC và ΔMNP có
\(\dfrac{AB}{MN}=\dfrac{AC}{MP}=\dfrac{BC}{NP}\left(=\dfrac{1}{2}\right)\)
Do đó: ΔABC~ΔMNP
Câu 12:
a: Xét ΔAMC và ΔANB có
\(\dfrac{AM}{AN}=\dfrac{AC}{AB}\left(\dfrac{10}{8}=\dfrac{15}{12}\right)\)
\(\widehat{MAC}\) chung
Do đó: ΔAMC đồng dạng với ΔANB
b: Ta có: ΔAMC đồng dạng với ΔANB
=>\(\widehat{ACM}=\widehat{ABN}\)
Xét ΔHMB và ΔHNC có
\(\widehat{HBM}=\widehat{HCN}\)
\(\widehat{MHB}=\widehat{NHC}\)(hai góc đối đỉnh)
Do đó; ΔHMB đồng dạng với ΔHNC
=>\(\dfrac{HB}{HC}=\dfrac{BM}{CN}\)
=>\(HB\cdot CN=BM\cdot CH\)
Câu 10:
Xét ΔOAD và ΔOCB có
\(\dfrac{OA}{OC}=\dfrac{OD}{OB}\)
góc O chung
Do đó: ΔOAD~ΔOCB
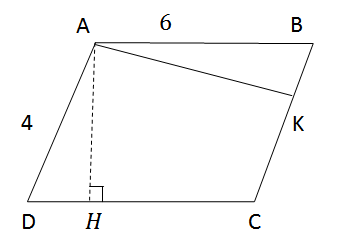
Xét hình bình bình ABCD có AB = CD = 8( cm ) và AD = BC = 6( cm )
Từ A kẻ các đường cao AH,AK.
Khi đó ta có:
Mà một hình bình hành thì chỉ có một diện tích chung nên 8.AH = 6.AK
Nếu độ dài đường cao thứ nhất là AH = 5( cm ) thì:
8.5 = 6.AK ⇔ AK = (8.5)/6 = 20/3( cm ) là độ dài đường cao thứ hai.
Nếu độ dài đường cao thứ nhất là AK = 5( cm ) thì:
8.AH = 6.5 ⇔ AH = (6.5)/8 = 15/4( cm ) là độ dài đường cao thứ hai.
Vậy bài toán này có hai đáp số