Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi x, y (giờ) lần lượt là thời gian mà một cần cẩu lớn và một cần cẩu nhỏ làm một mình xong công việc. Điều kiện: y > x > 4
Như vậy, trong 1 giờ cần cẩu lớn làm được 1/x (công việc), cần cẩu nhỏ làm được 1/y (công việc).
Trong 1 giờ, hai cần cẩu lớn và năm cần cẩu nhỏ làm được 1 : 4 = 1/4 (công việc)
Ta có phương trình: 2/x + 5/y = 1/4
Hai cần cẩu lớn làm trong 6 giờ và năm cần cẩu nhỏ làm trong 3 giờ nữa thì xong việc, ta có phương trình:
12/x + 15/y = 1
Ta có hệ phương trình:
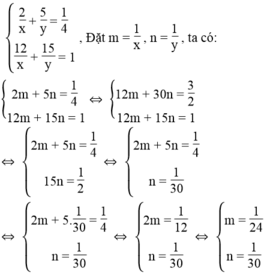
Ta có: 
⇔ x = 24
⇔ y = 30
Giá trị của x và y thỏa điều kiện bài toán.
Vậy một cần cẩu loại lớn làm xong công việc trong 24 giờ, một cần cẩu loại nhỏ làm xong công việc trong 30 giờ.
Gọi thời gian một cần cẩu lớn làm một mình xong việc là \(x\) (giờ), \(x>0\)
Gọi thời gian một cần cẩu lớn làm một mình xong việc là \(y\) (giờ), \(y>0\)
Gọi thời gian làm việc một mình xong việc của cần cầu bé là x (giờ) và cần cẩu lớn là y (giờ) với x;y>0
Trong mỗi giờ một cần cẩu bé làm được \(\dfrac{1}{x}\) phần công việc, một cần cẩu lớn làm được \(\dfrac{1}{y}\) phần công việc
Do 7 cần cẩu cùng làm thì 4 giờ xong việc nên:
\(4.\left(5.\dfrac{1}{x}+2.\dfrac{1}{y}\right)=1\Rightarrow\dfrac{5}{x}+\dfrac{2}{y}=\dfrac{1}{4}\)
Do 5 cần cầu bé làm 2 giờ sau đó 2 cần cẩu lớn cùng làm 3 giờ là xong nên:
\(2.\dfrac{5}{x}+3\left(\dfrac{5}{x}+\dfrac{2}{y}\right)=1\Rightarrow\dfrac{25}{x}+\dfrac{6}{y}=1\)
Ta được hệ: \(\left\{{}\begin{matrix}\dfrac{5}{x}+\dfrac{2}{y}=\dfrac{1}{4}\\\dfrac{25}{x}+\dfrac{6}{y}=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{40}\\\dfrac{1}{y}=\dfrac{1}{16}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=40\\y=16\end{matrix}\right.\)
Gọi xx (giờ) là thời gian một cần cẩu lớn làm xong việc, yy (giờ) là thời gian một cần cẩu bé làm xong việc (x,yx,y là các số dương).
- Cả năm cần cẩu cùng làm việc từ đầu thì sau 4\frac{6}{11}4116 giờ xong việc nên: \frac{2}{x}+\frac{3}{y}=1:4\frac{6}{11}=\frac{11}{50}x2+y3=1:4116=5011.
- Sau 1 giờ thì hai cần cẩu lớn làm được 1.\frac{2}{x}1.x2 công việc.
- Sau \frac{45}{11}1145 giờ thì cả năm cần cẩu làm được \frac{45}{11}.\left(\frac{2}{x}+\frac{3}{y}\right)1145.(x2+y3) công việc.
⇒ 1.\frac{2}{x}+\frac{45}{11}.\left(\frac{2}{x}+\frac{3}{y}\right)=1\Leftrightarrow\frac{56}{11}.\frac{2}{x}+\frac{45}{11}.\frac{3}{y}=1.1.x2+1145.(x2+y3)=1⇔1156.x2+1145.y3=1.
Ta thu được hệ phương trình: \left\{{}\begin{matrix}\frac{2}{x}+\frac{3}{y}=\frac{11}{50}\\\frac{56}{11}.\frac{2}{x}+\frac{45}{11}.\frac{3}{y}=1\end{matrix}\right.{x2+y3=50111156.x2+1145.y3=1.
Đặt u=\frac{2}{x};\quad v=\frac{3}{y}u=x2;v=y3, hệ phương trình trở thành: \left\{{}\begin{matrix}u+v=\frac{11}{50}\\\frac{56}{11}u+\frac{45}{11}v=1\end{matrix}\right.{u+v=50111156u+1145v=1.
Ta tìm được u=\frac{1}{10};\quad v=\frac{3}{25}\Rightarrow\quad x=20;\quad y=25.u=101;v=253⇒x=20;y=25.
Số phần công việc hai người công nhân làm trong 1 giờ là
1 : 8 = 1/8 ( công việc )
Số phần công việc người thứ nhất làm nhiều hơn người thứ hai trong 1 giờ là
1 : 12 = 1/12 ( công việc )
Trong 1 giờ người thứ nhất làm được số phần công việc là
( 1/8 - 1/12 ) : 2 = 1/48 ( công việc )
Số thời gian người thứ nhất làm xong công việc là
1: 1/48 = 48 ( giờ )
Số thời gian người thứ hai làm xong công việc là
48 - 12 = 36 ( giờ )
ĐS NT1 48 gio
NT2 36 giờ
Gọi x là năng suất mà tổ (I) làm trong 1h(x>0) (công việc/h)
y là năng suất mà tổ (II) làm trong 1h (y>0) (công việc/h)
Mà tổ (I)và (II) cùng làm với nhau trong 12h thì xong 1 công việc nên ta có phương trình:
12x+12y=1 (1)
nếu 2 tổ làm trong 3h sau đó tổ II đi làm việc khác và tổ I làm thêm 7h thì được 7/12 công việc nên
10x+3y=7/12 (2)
(1),(2) ta có hệ phương trình:
12x+12y=1
10x+3y=7/12
⇒x=1/21(TM); y=1/28(TM)
Vậy Tổ (I)làm một mình trong 21h thì xong công việc.
Tổ (II) làm một mình trong 28h thì xong công việc.