Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) tứ giác ABOC là hình vuông
vì BAC = 90 (giả thiết)
ABO = 90 (AB là tiếp tuyến)
ACO = 90 (AC là tiếp tuyến)
AB = AC (tính chất 2 tiếp tuyến cắt nhau)

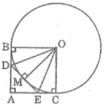
Theo tính chất của hai tiếp tuyến cắt nhau ta có :
DB = DM
EM = EC
Chu vi của tam giác ADE bằng :
AD + DE + EA = AD + DM + ME + EA
= AD + DB + AE + EC = AB + AC = 2AB
Mà tứ giác ABOC là hình vuông (chứng minh trên) nên:
AB = OB = 2 (cm)
Vậy chu vi của tam giác ADE bằng: 2.2 = 4 (cm)

Giải thích các bước giải:
MO là t.p.g. của AMBˆAMB^
⇒AMOˆ=BMOˆ=AMBˆ2=450⇒AMO^=BMO^=AMB^2=450
⇒ΔAMO−và−ΔBMO⇒ΔAMO−và−ΔBMO vuông cân
=> OA = AM = MB = BO
=> OAMB là h.thoi có AMBˆ=900AMB^=900
=> OAMB là h.v.
b)
PMPQ=MP+MQ+PQPMPQ=MP+MQ+PQ
=(MP+PC)+(MQ+QC)=(MP+PC)+(MQ+QC)
=(MP+PA)+(MQ+QB)=(MP+PA)+(MQ+QB)
=MA+MB=MA+MB
=2OA=2OA
=2R=2R
c)
OP−là−t.p.g.−của−AOCˆOP−là−t.p.g.−của−AOC^
⇒COPˆ=12AOCˆ⇒COP^=12AOC^ (1)
OQ−là−t.p.g.−của−BOCˆOQ−là−t.p.g.−của−BOC^
⇒COQˆ=12BOCˆ⇒COQ^=12BOC^ (2)
Cộng theo vế của (1) và (2), ta có:
COPˆ+COQˆ=12(AOCˆ+BOCˆ)=12AOBˆCOP^+COQ^=12(AOC^+BOC^)=12AOB^
⇒POQˆ=450
Giải thích các bước giải:
MO là t.p.g. của AMBˆAMB^
⇒AMOˆ=BMOˆ=AMBˆ2=450⇒AMO^=BMO^=AMB^2=450
⇒ΔAMO−và−ΔBMO⇒ΔAMO−và−ΔBMO vuông cân
=> OA = AM = MB = BO
=> OAMB là h.thoi có AMBˆ=900AMB^=900
=> OAMB là h.v.
b)
PMPQ=MP+MQ+PQPMPQ=MP+MQ+PQ
=(MP+PC)+(MQ+QC)=(MP+PC)+(MQ+QC)
=(MP+PA)+(MQ+QB)=(MP+PA)+(MQ+QB)
=MA+MB=MA+MB
=2OA=2OA
=2R=2R
c)
OP−là−t.p.g.−của−AOCˆOP−là−t.p.g.−của−AOC^
⇒COPˆ=12AOCˆ⇒COP^=12AOC^ (1)
OQ−là−t.p.g.−của−BOCˆOQ−là−t.p.g.−của−BOC^
⇒COQˆ=12BOCˆ⇒COQ^=12BOC^ (2)
Cộng theo vế của (1) và (2), ta có:
COPˆ+COQˆ=12(AOCˆ+BOCˆ)=12AOBˆCOP^+COQ^=12(AOC^+BOC^)=12AOB^
⇒POQˆ=450vv
