Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

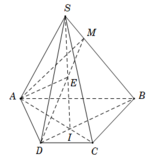
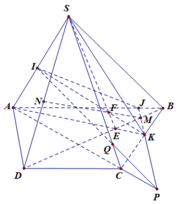
Ta có A là điểm chung thứ nhất của (ADM) và (SAC).
Trong mặt phẳng (BSD), gọi giao điểm của SI và DM là E.
Ta có:
+ E thuộc SI mà S I ⊂ S A C suy ra E ∈ S A C .
+ E thuộc DM mà D M ⊂ A D M suy ra E ∈ A D M .
Do đó E là điểm chung thứ hai của (ADM) và (SAC).
Vậy AE là giao tuyến của (ADM) và (SAC).
Chọn B.

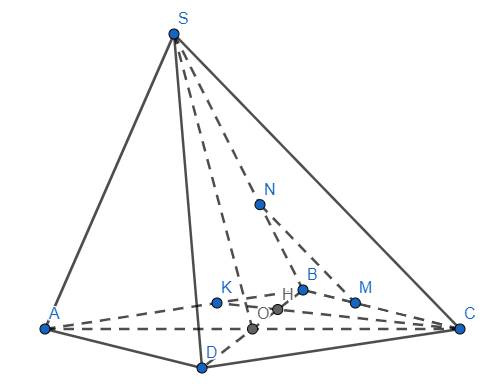
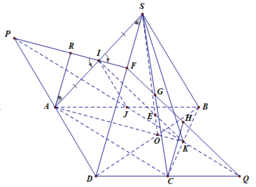
a) Ta có \(\left\{{}\begin{matrix}S\subset\left(SAC\right)\\S\subset\left(SBD\right)\end{matrix}\right.\)
và \(\left\{{}\begin{matrix}O\in AC\subset\left(SAC\right)\\O\in BD\subset\left(SBD\right)\end{matrix}\right.\) nên SO chính là giao tuyến của (SAC) và (SBD)
b) Trong mp(ABCD) cho CK cắt BD tại H. Do \(BD\subset\left(SBD\right)\) nên H cũng là giao điểm của CK và (SBD).
c) Vì \(\dfrac{BN}{NS}=\dfrac{BM}{MC}=\dfrac{1}{2}\) \(\Rightarrow\) MN//SC (Thelas đảo)
\(\Rightarrow\) MN//(SAC)

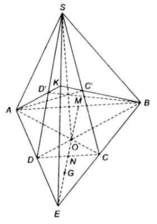
a) Gọi N là giao điểm của EM và CD
Vì M là trung điểm của AB nên N là trung điểm của CD (do ABCD là hình thang)
⇒ EN đi qua G
⇒ S, E, M, G ∈ (α) = (SEM)
Gọi O là giao điểm của AC và BD
Ta có (α) ∩ (SAC) = SO
và (α) ∩ (SBD) = SO = d
b) Ta có: (SAD) ∩ (SBC) = SE
c) Gọi O' = AC' ∩ BD'
Ta có AC' ⊂ (SAC), BD' ⊂ (SBD)
⇒ O' ∈ SO = d = (SAC) ∩ (SBD)

1: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
=>\(\left(SAC\right)\cap\left(SBD\right)=SO\)
AB//CD
S thuộc (SAB) giao (SCD)
=>(SAB) giao (SCD)=xy, xy qua S, xy//AB//DC
2:
Xét ΔSBC có SM/SB=SN/SC
nên MN//BC
=>MN//AD
=>AMND là hình thang
Xét ΔSBD có BM/BS=BO/BD
nên MO//SD
=>MO//(SAD)