Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(f'\left(x\right)=1-\dfrac{1}{x^2}=\dfrac{x^2-1}{x^2}>0;\forall x\ge2\)
\(\Rightarrow f\left(x\right)\) đồng biến
\(\Rightarrow f\left(x\right)_{min}=f\left(2\right)=\dfrac{5}{2}\)
* Hàm số đã cho liên tục trên R vì với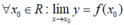 
nên (1) đúng
* Tại điểm x = 0 hàm số không có đạo hàm nên (2) sai.
* y = x 2 - 2 | x | + 2 = | x | 2 - 2 | x | + 2 = ( | x | - 1 ) 2 + 1 ≥ 1 ∀ x
Suy ra, GTNN của hàm số là 1 khi |x| = 1 ⇔ x = ±1
nên hàm số không có GTLN.
* Phương trình x 2 - 2 | x | + 2 = 0 vô nghiệm nên đồ thị không cắt trục hoành.
f ( - x ) = ( - x ) 2 - 2 | - x | + 2 = x 2 - 2 | x | + 2 = f ( x )
Nên hàm số đã cho là hàm số chẵn.
Mệnh đề 1, 5 đúng. Mệnh đề 2, 3,4,6 sai.
Chọn B
Đặt \(log_3\left(x+y\right)=log_2\left(x^3+y^3\right)=a\Rightarrow\left\{{}\begin{matrix}x+y=3^a\\x^3+y^3=2^a\end{matrix}\right.\)
\(2^a=\left(x+y\right)^3-3xy\left(x+y\right)=3^{3a}-3^{a+1}xy\)
\(\Rightarrow xy=\frac{3^{3a}-2^a}{3^{a+1}}\)
Mặt khác \(\left(x+y\right)^2\ge4xy\Rightarrow3^{2a}\ge\frac{4\left(3^{3a}-2^a\right)}{3^{a+1}}\)
\(\Leftrightarrow3^{3a+1}\ge4.3^{3a}-2^{a+2}\)
\(\Leftrightarrow2^{a+2}\ge3^{3a}\)
\(\Leftrightarrow\left(a+2\right)ln2\ge3a.ln3\)
\(\Rightarrow a\le\frac{2ln2}{3ln3-ln2}\)
\(\Rightarrow x+y=3^a< 2\) \(\Rightarrow x=1\)
Có duy nhất 1 số nguyên dương x
1.
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
\(y\left(0\right)=5;\) \(y\left(1\right)=3;\) \(y\left(2\right)=7\)
\(\Rightarrow y_{min}=3\)
2.
\(y'=4x^3-8x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-\sqrt{2}\end{matrix}\right.\)
\(f\left(-2\right)=-3\) ; \(y\left(0\right)=-3\) ; \(y\left(-\sqrt{2}\right)=-7\) ; \(y\left(1\right)=-6\)
\(\Rightarrow y_{max}=-3\)
3.
\(y'=\frac{\left(2x+3\right)\left(x-1\right)-x^2-3x}{\left(x-1\right)^2}=\frac{x^2-2x-3}{\left(x-1\right)^2}=0\Rightarrow x=-1\)
\(y_{max}=y\left(-1\right)=1\)
4.
\(y'=\frac{2\left(x^2+2\right)-2x\left(2x+1\right)}{\left(x^2+2\right)^2}=\frac{-2x^2-2x+4}{\left(x^2+2\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
\(y\left(1\right)=1\) ; \(y\left(-2\right)=-\frac{1}{2}\Rightarrow y_{min}+y_{max}=-\frac{1}{2}+1=\frac{1}{2}\)
Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng
Chọn B
Xét hàm số
Trên (1; +∞) y' = 0 => x = 2. Bảng biến thiên
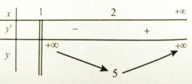
Giá trị nhỏ nhất của hàm số là y=5.
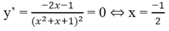
Chọn D
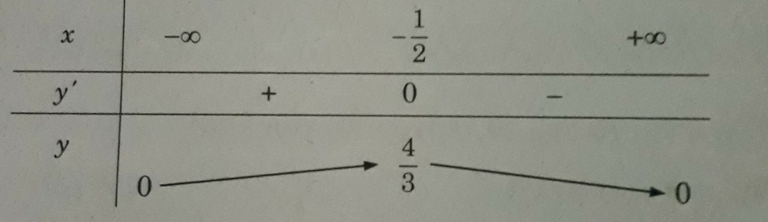
Xét hàm số
Ta có bảng biến thiên
Hàm số không có GTNN