Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(M>\frac{x}{x+y+z+t}+\frac{y}{x+y+z+t}+\frac{z}{x+y+z+t}+\frac{t}{x+y+z+t}=\frac{x+y+z+t}{x+y+z+t}=1\)
Mà \(\frac{a}{b}<1\) thì \(\frac{a}{b}<\frac{a+m}{b+m}\) ; \(m\in N\)*
Do đó \(M<\frac{x+t}{x+y+z+t}+\frac{y+z}{x+y+z+t}+\frac{z+x}{x+y+z+t}+\frac{t+y}{x+y+z+t}=\frac{2\left(x+y+z+t\right)}{x+y+z+t}=2\)
Vậy 1 < M < 2 nên M không phải là số tự nhiên/

Giả sử đa diện (H) có các đỉnh là ![]() , gọi
, gọi ![]() lần lượt là số các mặt của (H) nhận chúng là đỉnh chung. Như vậy mỗi đỉnh
lần lượt là số các mặt của (H) nhận chúng là đỉnh chung. Như vậy mỗi đỉnh ![]() có
có ![]() cạnh đi qua. Do mỗi cạnh của (H) là cạnh chưn của đúng hai mặt nên tổng số các cạnh của H bằng
cạnh đi qua. Do mỗi cạnh của (H) là cạnh chưn của đúng hai mặt nên tổng số các cạnh của H bằng ![]()
Vì c là số nguyên, ![]() là những số lẻ nên Đ phải là số chẵn. Ví dụ : Số đỉnh của hình chóp ngũ giác bằng sáu.
là những số lẻ nên Đ phải là số chẵn. Ví dụ : Số đỉnh của hình chóp ngũ giác bằng sáu.

Đáp án C
Cách 1:
Dựa vào hình vẽ ta đếm được số
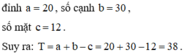
Cách 2:
Đa diện ở hình vẽ là hình đa diện đều 12 mặt.
Nên ta có các thông số về số đỉnh, số cạnh, số mặt lần lượt là 20,30,12.
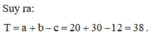
 bit lm bài này k giup tui
bit lm bài này k giup tui
Đáp án A
Đây là hình bát diện đều có 6 đỉnh,12 cạnh,8 mặt do đó x + y + 2 z = 34.