Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
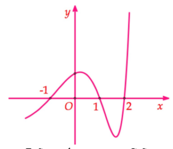
Phương pháp : Ứng dụng tích phân để tính diện tích hình phẳng.
Cách giải:
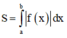
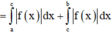
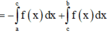

Ta có
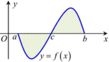
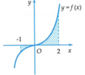
S = ∫ - 1 2 f x d x = ∫ - 1 1 f x d x + ∫ 1 2 f x d x = ∫ - 1 1 f x d x + ∫ - 1 1 - f ( x ) d x = a - b .
Chọn đáp án B.

Đáp án A
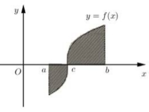
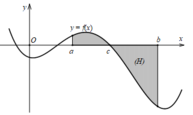
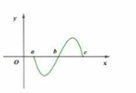
Từ hình trên S = ∫ a b f x dx = − ∫ a b f x dx → Đáp án B, C , D đúng.

Đáp án A
Phương pháp:
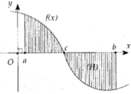
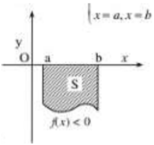
Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a, x= b (a<b) được tính theo công thức S = ∫ a b f ( x ) d x
Cách giải:
Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a, x= b (a<b) được tính theo công thức S = ∫ a b f ( x ) d x
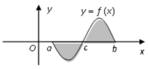
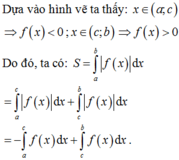

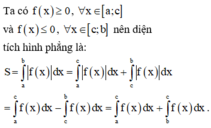

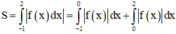
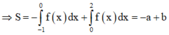
Đáp án C.