Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

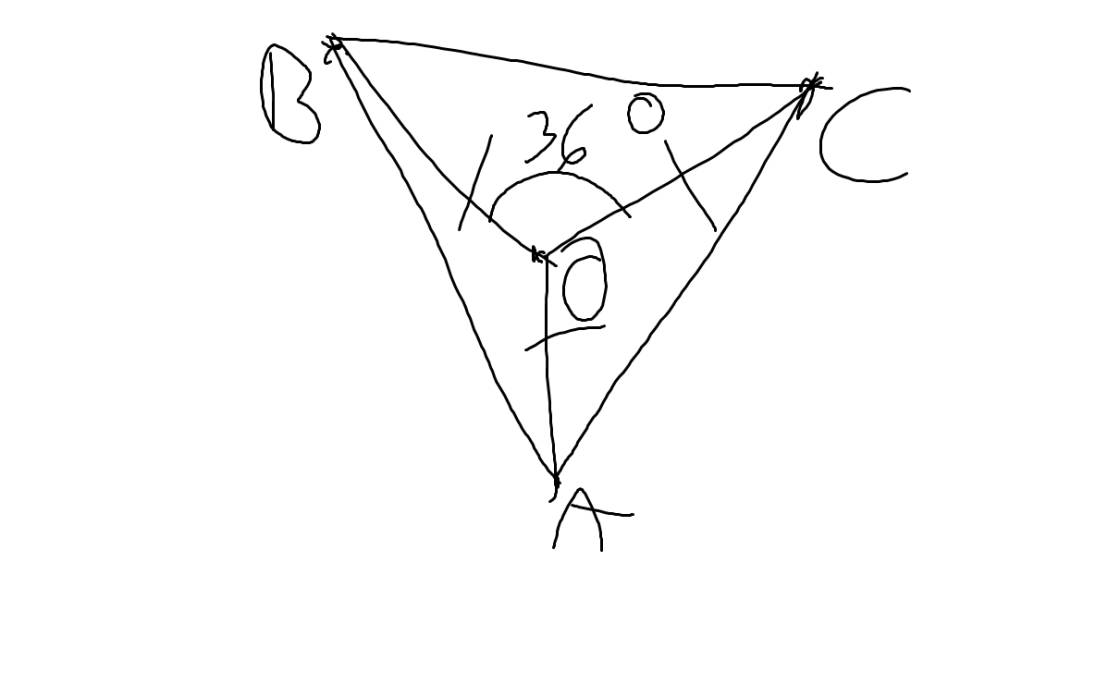
Gọi B,C lần lượt là các cọc gôn,A là điểm cách chấm phạt đền 11,6m, O là chấm phạt đền
Theo đề, ta có: OA=OB=OC=11,6(m) và \(\widehat{BOC}=36^0\)
=>O là tâm đường tròn ngoại tiếp ΔABC
Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
=>\(\widehat{BAC}=\dfrac{1}{2}\cdot\widehat{BOC}\)
=>\(\widehat{BAC}=\dfrac{1}{2}\cdot36^0=18^0\)

Gọi A là chân tường, C là chân thang và B là đỉnh thang
Xét tam giác ABC vuông tại A:
\(cosC=\dfrac{AC}{BC}=\dfrac{5}{13}\Rightarrow\widehat{C}\approx67^0\)

Đây là toán lớp 5 thì phải? Nhảy qua bên lớp 9 giải pt hoặc hệ là ráng chịu nhaa =))
ta coi số thóc mẹ khuê đem ra phơi là 100%.bị hao mất 5% thì còn lại số % là:100%-5%=95%
lúc đầu đem ra phơi là:4351*100 :95=4580
đúng 100% luôn mình làm rồi
Gọi B là góc tạo bởi tia nắng, bóng trên mặt đất là AB và C là đỉnh cột cờ
Áp dụng tslg trong tam giác ABC vuông tại A:
\(tanB=\dfrac{AC}{AB}\Rightarrow AC=4,5.tan53^0\approx6\left(m\right)\)