Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
\(\cos225^0=\cos\left(180^0+45^0\right)=-\cos45^0=-\dfrac{\sqrt{2}}{2}\)
\(\sin240^0=\sin\left(180^0+60^0\right)=-\sin60^0=-\dfrac{\sqrt{3}}{2}\)
\(\cos\left(-15^0\right)=-\cot15^0=-\tan75^0=-\tan\left(30^0+45^0\right)\)
\(=\dfrac{-\tan30^0-\tan45^0}{1-\tan30^0\tan45^0}=\dfrac{-\dfrac{1}{\sqrt{3}}-1}{1-\dfrac{1}{\sqrt{3}}}=-\dfrac{\sqrt{3}+1}{\sqrt{3}-1}\)
\(=-\dfrac{\left(\sqrt{3}+1\right)^2}{2}=-2-\sqrt{3}\)
\(\tan75^0=\cot15^0=2+\sqrt{3}\)
b)
\(\sin\dfrac{7\pi}{12}=\sin\left(\dfrac{\pi}{3}+\dfrac{\pi}{4}\right)=\sin\dfrac{\pi}{3}\cos\dfrac{\pi}{4}+\cos\dfrac{\pi}{3}\sin\dfrac{\pi}{4}\)
\(=\dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}\right)=\dfrac{\sqrt{6}+\sqrt{2}}{4}\)
\(\cos\left(-\dfrac{\pi}{12}\right)=\cos\left(\dfrac{\pi}{4}-\dfrac{\pi}{3}\right)=\cos\dfrac{\pi}{4}\cos\dfrac{\pi}{3}+\sin\dfrac{\pi}{3}\sin\dfrac{\pi}{4}\)
\(=\dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}\right)=0,9659\dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}\right)=0,9659\)
\(\tan\dfrac{13\pi}{12}=\tan\left(\pi+\dfrac{\pi}{12}\right)=\tan\dfrac{\pi}{12}=\tan\left(\dfrac{\pi}{3}-\dfrac{\pi}{4}\right)\)
\(=\dfrac{\tan\dfrac{\pi}{3}-\tan\dfrac{\pi}{4}}{1+\tan\dfrac{\pi}{3}\tan\dfrac{\pi}{4}}=\dfrac{\sqrt{3}-1}{1+\sqrt{3}}=2-\sqrt{3}\)

đề sai nhỉ? sina/2; cos a/2; tana/2; cota/2 chứ?
ta có:
\(sin^2\dfrac{a}{2}=\dfrac{1-cosa}{2}=\dfrac{1-\dfrac{5}{13}}{2}=\dfrac{4}{13}\)
\(\dfrac{3\pi}{2}< a< 2\pi\Leftrightarrow\dfrac{3\pi}{4}< \dfrac{a}{2}< \pi\)
=> sina/2 > 0 => sina/2 = \(\dfrac{2}{\sqrt{13}}\)
ta có:
\(cos^2\left(\dfrac{a}{2}\right)=1-sin^2\left(\dfrac{a}{2}\right)=1-\dfrac{4}{13}=\dfrac{9}{13}\)
\(\dfrac{3\pi}{2}< a< 2\pi\Leftrightarrow\dfrac{3\pi}{4}< \dfrac{a}{2}< \pi\) (cung2)
=> cosa/2 < 0 => cosa/2 = \(\dfrac{-3}{\sqrt{13}}\)
\(tan\left(\dfrac{a}{2}\right)=\dfrac{sin\left(\dfrac{a}{2}\right)}{cos\left(\dfrac{a}{2}\right)}=\dfrac{\dfrac{2}{\sqrt{13}}}{-\dfrac{3}{\sqrt{13}}}=-\dfrac{2}{3}\)
\(cot\left(\dfrac{a}{2}\right)=\dfrac{1}{tan\left(\dfrac{a}{2}\right)}=\dfrac{1}{-\dfrac{2}{3}}=-\dfrac{3}{2}\)
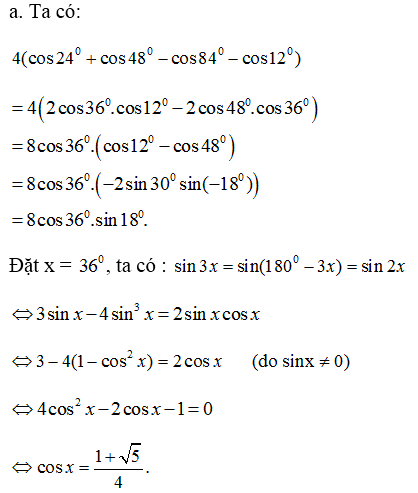
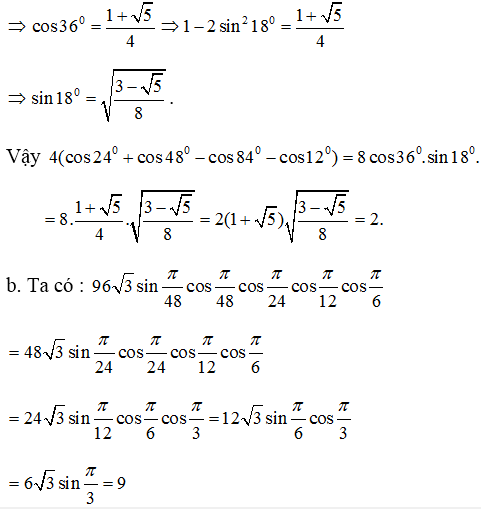
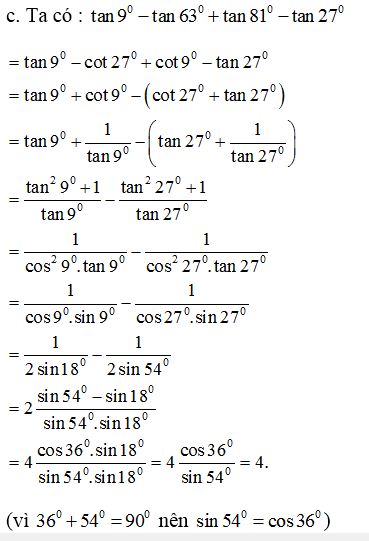
\(\cos\dfrac{\pi}{15}.\cos\dfrac{2\pi}{15}...\cos\dfrac{7\pi}{15}=-\dfrac{1}{2}.\left(\cos\dfrac{\pi}{15}.\cos\dfrac{2\pi}{15}.\cos\dfrac{4\pi}{15}.\cos\dfrac{8\pi}{15}\right).\left(\cos\dfrac{3\pi}{15}.\cos\dfrac{6\pi}{15}\right)\)
\(=-\dfrac{1}{2}.\left(\cos\dfrac{\pi}{15}.\cos\left(2.\dfrac{\pi}{15}\right).\cos\left(2^2.\dfrac{\pi}{15}\right).\cos\left(2^3\dfrac{\pi}{15}\right)\right).\left(\cos\dfrac{3\pi}{15}.\cos\left(2.\dfrac{3\pi}{15}\right)\right)\)
\(=-\dfrac{1}{2}.\left(\dfrac{\sin\left(2^4.\dfrac{\pi}{15}\right)}{16.\sin\left(\dfrac{\pi}{15}\right)}\right).\left(\dfrac{\sin\left(2^2\dfrac{3\pi}{15}\right)}{4.\sin\left(\dfrac{3\pi}{15}\right)}\right)\)
\(=-\dfrac{1}{2}.\left(\dfrac{\sin\left(\dfrac{16\pi}{15}\right)}{16.\sin\left(\dfrac{\pi}{15}\right)}\right).\left(\dfrac{\sin\left(\dfrac{12\pi}{15}\right)}{4.\sin\left(\dfrac{3\pi}{15}\right)}\right)\)
\(=-\dfrac{1}{2}.\left(\dfrac{-\sin\left(\dfrac{\pi}{15}\right)}{16.\sin\left(\dfrac{\pi}{15}\right)}\right).\left(\dfrac{\sin\left(\dfrac{3\pi}{15}\right)}{4.\sin\left(\dfrac{3\pi}{15}\right)}\right)=\dfrac{1}{128}\)