
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
45 phút=3/4 giờ
Bài 5:
x+3/10=-2/5
=>x=-2/5-3/10=-7/10
Bài 6:
\(=\dfrac{3^9\cdot5^{11}\left(5-3^2\right)}{5^{10}\cdot3^{10}}=\dfrac{5\cdot\left(-4\right)}{3}=-\dfrac{20}{3}\)


a,trên cùng một nửa mặt phẳng bờ chứa tia Ox ta có:
góc xOy>góc xOz (80độ>30độ)
=>Oz nằm giữa hai tia Ox,Oy
b,vì Oz nằm giữa hai tia Ox,Oy
góc zOy+góc zOx=góc yOx
góc zOy+30độ=80độ
góczOy =80độ-30độ
góc zOy =50độ
c,vì góc yOt và góc xOy là góc kề bù
góc yOt + góc yOx=180độ
góc yOt+80độ=180 độ
góc yOt =180 độ -80độ
góc yOt =100độ
vì góc zOt và góc zOx là góc kề bù
góc zOt+góc zOx=180độ
góc zOt+30 độ=180độ
góc zOt =180 độ -30độ
góc zOt =150độ
a)Vì Oy, Oz nằm trên cùng một nửa mặt phẳng bờ chứa tia Ox
Mà \(\widehat{xOz}< \widehat{xOy}\)
Do đó tia Oz nằm giữa hai tia Ox và Oy.
b)\(\widehat{zOy}=\widehat{xOy}-\widehat{xOz}=80^o-30^o=50^o.\)
c) Ot là tia đối của tia Ox nên \(\widehat{xOy}+\widehat{yOt}=180^o\)
Vậy \(\widehat{yOt}=180^o-\widehat{xOt}=180^o-80^o=100^o\)
\(\widehat{zOt}=\widehat{zOy}+\widehat{yOt}=50^o+100^o=150^o.\)

Chúc em học tốt!

a: \(=\dfrac{2^5\cdot\left(9-2\right)}{2^5\left(5+9\right)}=\dfrac{7}{14}=\dfrac{1}{2}\)
b: =1/3-1/7=4/21
c: \(=\dfrac{32}{56}-\dfrac{35}{56}-\dfrac{6}{56}=\dfrac{-9}{56}\)
d: \(=\dfrac{-39}{90}+\dfrac{34}{90}-\dfrac{35}{90}=-\dfrac{40}{90}=-\dfrac{4}{9}\)

\(\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{x\left(x+1\right)}=\frac{2}{5}\)
\(\Rightarrow\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{x}-\frac{1}{x+1}=\frac{2}{5}\)
\(\Rightarrow\frac{1}{2}-\frac{1}{x+1}=\frac{2}{5}\)
\(\Rightarrow\frac{1}{x+1}=\frac{1}{2}-\frac{2}{5}\)
\(\Rightarrow\frac{1}{x+1}=\frac{1}{10}\)
=> x+1=10
=>x=9

\(A=\dfrac{2}{1.2}+\dfrac{2}{2.3}+\dfrac{2}{3.4}+...+\dfrac{2}{99.100}\)
\(A=2\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}\right)\)
\(A=2\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{98}-\dfrac{1}{99}+\dfrac{1}{99}-\dfrac{1}{100}\right)\)
\(A=2\left(1-\dfrac{1}{100}\right)\)
\(A=2.\dfrac{99}{100}\)
\(A=\dfrac{99}{50}\)
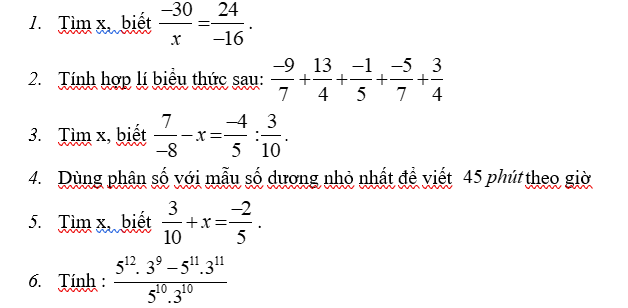 Giúp với ạ cần gấp lắm sắp thi rồi!!!!!!!!!!!!!!
Giúp với ạ cần gấp lắm sắp thi rồi!!!!!!!!!!!!!!




 rồi
rồi 