Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D

Gọi N, K là trung điểm của BB', A'B'
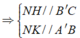
![]()
Ta tính được
![]()
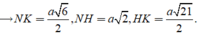
Áp dụng định lí hàm cosin ta suy ra

Cách 2. Chọn hệ trục tọa độ Oxyz với
![]()
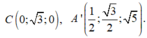
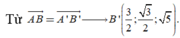

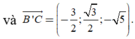
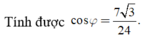

Đáp án A.
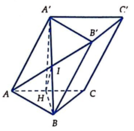
Ta có ![]() => A'H = BH = a
=> A'H = BH = a
Gọi ![]()
HI//B'C' (tính chất đường trung bình)
=> A'B ⊥ B'C

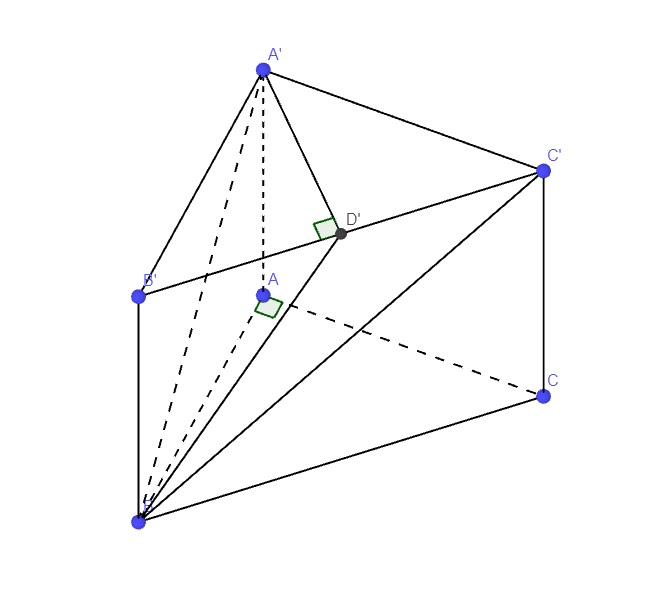
\(A'A\perp\left(ABC\right)\) theo giả thiết \(\Rightarrow\widehat{A'BA}\) là góc giữa A'B và đáy
\(\Rightarrow tan\widehat{A'BA}=2\Rightarrow A'A=AB.tan\widehat{A'BA}=2a\)
a.
Gọi D' là trung điểm B'C' \(\Rightarrow A'D'\perp B'C'\) (đáy là tam giác vuông cân)
\(\Rightarrow A'D'\perp\left(BCC'B'\right)\Rightarrow\widehat{A'BD'}\) là góc giữa A'B và (BCC'B')
\(A'B=\sqrt{AB^2+A'A^2}=a\sqrt{5}\)
\(A'D'=\dfrac{1}{2}B'C'=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow sin\widehat{A'BD'}=\dfrac{A'D'}{A'B}=\dfrac{\sqrt{10}}{10}\Rightarrow\widehat{A'BD'}\approx18^026'\)
b.
\(\left\{{}\begin{matrix}A'C'\perp A'B'\left(gt\right)\\A'A\perp\left(A'B'C'\right)\Rightarrow A'A\perp A'C'\end{matrix}\right.\)
\(\Rightarrow A'C'\perp\left(ABB'A'\right)\Rightarrow\widehat{C'BA'}\) là góc giữa C'B và (ABB'A')
\(tan\widehat{C'BA'}=\dfrac{A'C'}{A'B}=\dfrac{a}{a\sqrt{5}}=\dfrac{1}{\sqrt{5}}\)
\(\Rightarrow\widehat{C'BA'}\approx24^06'\)

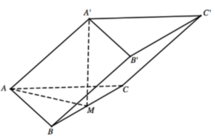
a) \(BCC'B'\) là hình chữ nhật \( \Rightarrow BC\parallel B'C'\)
\( \Rightarrow \left( {AB,B'C'} \right) = \left( {AB,BC} \right) = \widehat {ABC} = {60^ \circ }\).
b)
\(\Delta AA'B\) vuông tại \(A \Rightarrow \tan \widehat {ABA'} = \frac{{AA'}}{{AB}} = \frac{a}{a} = 1 \Rightarrow \widehat {ABA'} = {45^ \circ }\)
Vậy \(\left( {A'B,\left( {ABC} \right)} \right) = {45^ \circ }\).
c) \(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot BC,CC' \bot CM\)
Vậy \(\widehat {BCM}\) là góc nhị diện \(\left[ {B,CC',M} \right]\).
\(\Delta ABC\) đều \( \Rightarrow \widehat {BCM} = \frac{1}{2}\widehat {ACB} = {30^ \circ }\).
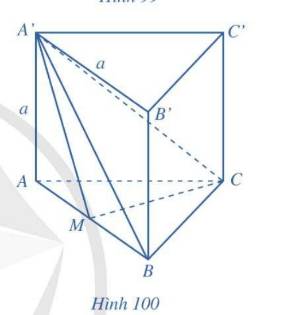
d) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CM\)
\(\Delta ABC\) đều \( \Rightarrow CM \bot AB\).
\( \Rightarrow CM \bot \left( {ABB'A'} \right)\)
\(\Delta ABC\) đều \( \Rightarrow CM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\).
\(\left. \begin{array}{l}CC'\parallel AA'\\AA' \subset \left( {ABB'A'} \right)\end{array} \right\} \Rightarrow CC'\parallel \left( {ABB'A'} \right)\)
\( \Rightarrow d\left( {CC',\left( {ABB'A'} \right)} \right) = d\left( {C,\left( {ABB'A'} \right)} \right) = CM = \frac{{a\sqrt 3 }}{2}\)
e) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CM\)
\(\Delta ABC\) đều \( \Rightarrow CM \bot AB\).
\( \Rightarrow CM \bot \left( {ABB'A'} \right) \Rightarrow CM \bot A'M\)
\(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot CM\)
\( \Rightarrow d\left( {CC',A'M} \right) = CM = \frac{{a\sqrt 3 }}{2}\)
g) \({S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4},h = AA' = a\)
\( \Rightarrow {V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{{a^2}\sqrt 3 }}{4}.a = \frac{{{a^3}\sqrt 3 }}{4}\)
\({S_{\Delta MBC}} = \frac{1}{2}{S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{8},h = AA' = a\)
\( \Rightarrow {V_{A'.MBC}} = \frac{1}{3}{S_{\Delta MBC}}.AA' = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{8}.a = \frac{{{a^3}\sqrt 3 }}{{24}}\)

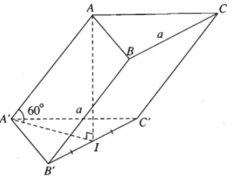
a) Gọi I là trung điểm của cạnh B'C'. Theo giả thiết ta có AI ⊥ (A'B'C') và ∠ A A ′ I = 60 ο . Ta biết rằng hai mặt phẳng (ABC) và (A'B'C') song song với nhau nên khoảng cách giữa hai mặt phẳng chính là khoảng cách AI.
Do đó
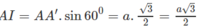
b) 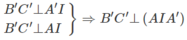
⇒ B′C′ ⊥ AA′
Mà AA′ // BB′ // CC′ nên B’C’ ⊥ BB’
Vậy mặt bên BCC’B’ là một hình vuông vì nó là hình thoi có một góc vuông.