
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(7\sqrt{2}+\sqrt{8}-\sqrt{32}\)
\(=7\sqrt{2}+2\sqrt{2}-4\sqrt{2}\)
\(=5\sqrt{2}\)
b: \(2\sqrt{5}-\sqrt{\left(2-\sqrt{5}\right)^2}\)
\(=2\sqrt{5}-\left|2-\sqrt{5}\right|\)
\(=2\sqrt{5}-\left(\sqrt{5}-2\right)\)
\(=2\sqrt{5}-\sqrt{5}+2=\sqrt{5}+2\)
c: \(\left(\dfrac{1}{3-\sqrt{5}}-\dfrac{1}{3+\sqrt{5}}\right)\cdot\dfrac{\sqrt{5}-1}{5-\sqrt{5}}\)
\(=\dfrac{3+\sqrt{5}-\left(3-\sqrt{5}\right)}{9-5}\cdot\dfrac{\sqrt{5}-1}{\sqrt{5}\left(\sqrt{5}-1\right)}\)
\(=\dfrac{3+\sqrt{5}-3+\sqrt{5}}{4}\cdot\dfrac{1}{\sqrt{5}}=\dfrac{2\sqrt{5}}{4\sqrt{5}}=\dfrac{1}{2}\)
d: \(\dfrac{10\sqrt{18}+5\sqrt{3}-15\sqrt{27}}{3\sqrt{2}-4\sqrt{3}}\)
\(=\dfrac{10\cdot3\sqrt{2}+5\sqrt{3}-15\cdot3\sqrt{3}}{3\sqrt{2}-4\sqrt{3}}\)
\(=\dfrac{30\sqrt{2}-40\sqrt{3}}{3\sqrt{2}-4\sqrt{3}}=\dfrac{10\left(3\sqrt{2}-4\sqrt{3}\right)}{3\sqrt{2}-4\sqrt{3}}=10\)

a. \(\sqrt{-2x+3}\)
ĐKXĐ: x < 0
b. \(\sqrt{\dfrac{2}{x^2}}\)
ĐKXĐ: x \(\ne\) 0
c. \(\sqrt{\dfrac{4}{x+3}}\)
ĐKXĐ: x > -3
d. \(\sqrt{\dfrac{-5}{x^2+6}}\)
ĐKXĐ: x vô nghiệm
4. a. x2 - 7
= x2 - \(\left(\sqrt{7}\right)^2\)
= \(\left(x-\sqrt{7}\right)\left(x+\sqrt{7}\right)\)
b. x2 - \(2\sqrt{2}x\) + 2
= x2 - \(2\sqrt{2}x\) + \(\left(\sqrt{2}\right)^2\)
= (x - \(\sqrt{2}\))2
c. x2 + \(2\sqrt{13}x\) + 13
= x2 + \(2\sqrt{13}x\) + \(\left(\sqrt{13}\right)^2\)
= \(\left(x+\sqrt{13}\right)^2\)


a: A(1;-3); B(2;4); C(-1;2)
\(AB=\sqrt{\left(2-1\right)^2+\left(4+3\right)^2}=5\sqrt{2}\)
\(BC=\sqrt{\left(-1-2\right)^2+\left(2-4\right)^2}=\sqrt{13}\)
\(AC=\sqrt{\left(-1-1\right)^2+\left(2+3\right)^2}=\sqrt{29}\)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+BC+AC=5\sqrt{2}+\sqrt{13}+\sqrt{29}\)
Xét ΔABC có
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
\(=\dfrac{50+29-13}{2\cdot5\sqrt{2}\cdot\sqrt{29}}=\dfrac{33}{5\sqrt{58}}\)
\(sin^2A+cos^2A=1\)
=>\(sin^2A=1-\left(\dfrac{33}{5\sqrt{58}}\right)^2=\dfrac{361}{1450}\)
=>\(sinA=\sqrt{\dfrac{361}{1450}}\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC=\dfrac{1}{2}\cdot\sqrt{\dfrac{361}{1450}\cdot50\cdot29}=\dfrac{19}{2}\)
b: Gọi (d): y=ax+b là phương trình đường thẳng AB
(d) đi qua A(1;-3) và B(2;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=-3\\2a+b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-a=-7\\a+b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=7\\b=-3-a=-3-7=-10\end{matrix}\right.\)
Vậy: (d): y=7x-10
c: Gọi (d1):y=ax+b là phương trình đường thẳng cần tìm
Vì (d1) vuông góc AB nên \(a\cdot7=-1\)
=>\(a=-\dfrac{1}{7}\)
=>(d1): \(y=-\dfrac{1}{7}x+b\)
Thay x=-1 và y=2 vào (d1), ta được:
\(b+\dfrac{1}{7}=2\)
=>\(b=2-\dfrac{1}{7}=\dfrac{13}{7}\)
Vậy: (d1): \(y=-\dfrac{1}{7}x+\dfrac{13}{7}\)


Bài 2:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{3.4}{5}=2,4$ (cm)
Áp dụng định lý Pitago:
$BH=\sqrt{AB^2-AH^2}=\sqrt{3^2-2,4^2}=1,8$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{4^2-2,4^2}=3,2$ (cm)
b.
Áp dụng hệ thức lượng trong tam giác vuông:
$AH^2=BH.CH=9.16$
$\Rightarrow AH=12$ (cm)
Áp dụng định lý Pitago:
$AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+9^2}=15$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20$ (cm)
$BC=BH+CH=9+16=25$ (cm)
Bài 3:
Vì $AB:AC=3:4$ nên đặt $AB=3a; AC=4a$ (cm)
Áp dụng định lý Pitago:
$15=BC=\sqrt{AB^2+AC^2}=\sqrt{(3a)^2+(4a)^2}=5a$
$\Rightarrow a=3$ (cm)
$AH=\frac{AB.AC}{BC}=\frac{3a.4a}{5a}=2,4a$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{(3a)^2-(2,4a)^2}=1,8a=1,8.3=5,4$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{(4a)^2-(2,4a)^2}=3,2a=3,2.3=9,6$ (cm)


a, ĐKXĐ : \(\left\{{}\begin{matrix}x\ne3\\x\ge1\end{matrix}\right.\)
Ta có : \(P=\dfrac{x-1-2}{\sqrt{x-1}-\sqrt{2}}=\dfrac{\left(\sqrt{x-1}-\sqrt{2}\right)\left(\sqrt{x-1}+\sqrt{2}\right)}{\sqrt{x-1}-\sqrt{2}}\)
\(=\sqrt{x-1}+\sqrt{2}\)
b, Thấy : \(\sqrt{x-1}\ge0\)
\(\Rightarrow P=\sqrt{x-1}+\sqrt{2}\ge\sqrt{2}\)
Vậy \(Min=\sqrt{2}\Leftrightarrow x=1\)
Vậy ,...
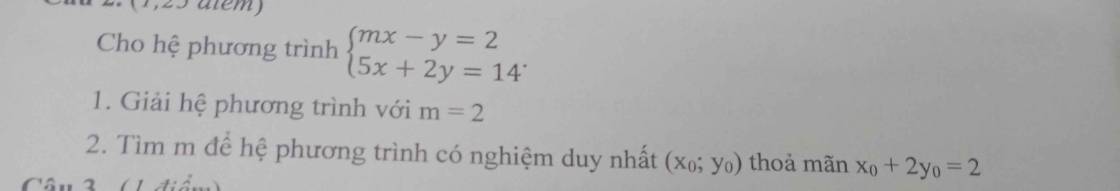


 mọi người giúp mình nhanh nhé mình cần gấp
mọi người giúp mình nhanh nhé mình cần gấp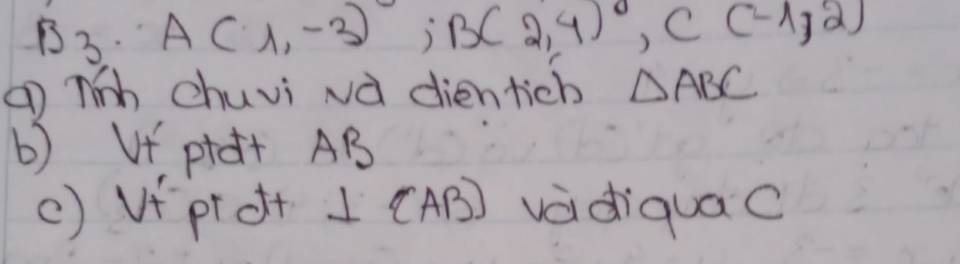


1: Thay m=2 vào hệ, ta được:
\(\left\{{}\begin{matrix}2x-y=2\\5x+2y=14\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x-2y=4\\5x+2y=14\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=18\\2x-y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=2x-2=2\cdot2-2=2\end{matrix}\right.\)
2: Để hệ có nghiệm duy nhất thì \(\dfrac{m}{5}\ne\dfrac{-1}{2}\)
=>\(m\ne-\dfrac{5}{2}\)
\(\left\{{}\begin{matrix}mx-y=2\\5x+2y=14\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2mx-2y=4\\5x+2y=14\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(2m+5\right)=18\\mx-y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{18}{2m+5}\\y=mx-2=\dfrac{18m}{2m+5}-2=\dfrac{18m-4m-10}{2m+5}=\dfrac{14m-10}{2m+5}\end{matrix}\right.\)
\(x+2y=2\)
=>\(\dfrac{18+28m-20}{2m+5}=2\)
=>\(28m-2=4m+10\)
=>24m=12
=>\(m=\dfrac{1}{2}\left(nhận\right)\)