
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\frac{x}{2}+\frac{3}{2}\sqrt{x^2-4x+4}-2=\frac{x}{2}+\frac{3}{2}\left|x-2\right|-2\)
Với x >= 2 thì \(\frac{x}{2}+\frac{3\left(x-2\right)}{2}=\frac{3x+x-6}{2}=\frac{4x-6}{2}=2x-3\)
Với x < 2 thì \(\frac{x}{2}+\frac{3\left(2-x\right)}{2}=\frac{x+6-3x}{2}=\frac{6-2x}{2}=3-x\)



a: \(\Leftrightarrow\left\{{}\begin{matrix}9x-3y=15\\2x+3y=18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=3x-5=4\end{matrix}\right.\)
mk cảm ơn bạn đã giúp mk nhưng mà bạn làm chi tiết giùm mk nhé



Câu 2b
\(\left\{{}\begin{matrix}2x+y=5\\2x-6y=14m-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7y=5-14m+2\\x=\dfrac{5-y}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1-2m\\x=\dfrac{5-1+2m}{2}=2+m\end{matrix}\right.\)
Ta có \(2\left(m+2\right)^2-\left(2m-1\right)^2=17\)
\(\Leftrightarrow2m^2+8m+8-4m^2+4m-1=17\Leftrightarrow-2m^2+12m-10=0\)
Ta có a + b + c = -2 + 12 - 10 = 0
vậy pt có 2 nghiệm m = 1 ; m = 5
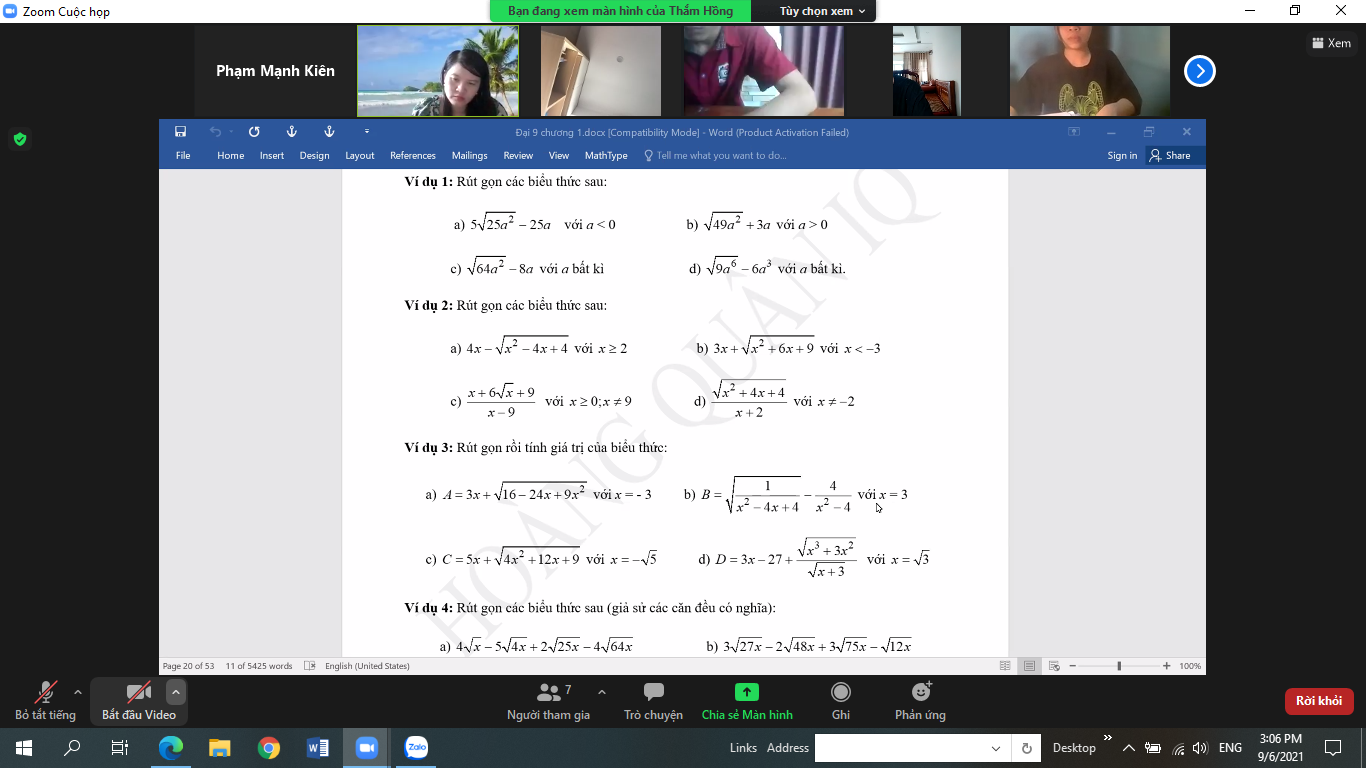
 giúp mk vs mk cần gấp
giúp mk vs mk cần gấp

 giúp mk vs mk cần gấp
giúp mk vs mk cần gấp

