K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QN
0
6 tháng 2 2023
Bài 1:
a: Đặt 14,4-3,6t^2=0
=>3,6t^2=14,4
=>t^2=4
=>t=2
b: TXĐ: [0;2]
TGT: [0;14,4]
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 7 2021
a.
\(sin^4a+cos^4a=\left(sin^2a+cos^2a\right)^2-2sin^2a.cos^2a\)
\(=1-\dfrac{1}{2}\left(2sina.cosa\right)^2=1-\dfrac{1}{2}sin^22a\)
\(=1-\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{2}cos4a\right)=\dfrac{3}{4}+\dfrac{1}{4}cos4a\)
b.
\(sin^6a+cos^6a=\left(sin^2a+cos^2a\right)^2-3sin^2a.cos^2a\left(sin^2a+cos^2a\right)\)
\(=1-3sin^2a.cos^2a=1-\dfrac{3}{4}\left(2sina.cosa\right)^2\)
\(=1-\dfrac{3}{4}sin^22a=1-\dfrac{3}{4}\left(\dfrac{1}{2}-\dfrac{1}{2}cos4a\right)\)
\(=\dfrac{5}{8}+\dfrac{3}{8}cos4a\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 7 2021
e.
\(\dfrac{cos2a}{1+sin2a}=\dfrac{cos^2a-sin^2a}{sin^2a+cos^2a+2sina.cosa}=\dfrac{\left(cosa-sina\right)\left(cosa+sina\right)}{\left(sina+cosa\right)^2}=\dfrac{cosa-sina}{cosa+sina}\)
f.
\(cotx+tanx=\dfrac{cosx}{sinx}+\dfrac{sinx}{cosx}\)
\(=\dfrac{sin^2x+cos^2x}{sinx.cosx}=\dfrac{1}{sinx.cosx}\)
\(=\dfrac{2}{2sinx.cosx}=\dfrac{2}{sin2x}\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 9 2021
\(y=\dfrac{2x^2-6x+10}{2\left(x^2+1\right)}=\dfrac{11\left(x^2+1\right)-9x^2-6x-1}{2\left(x^2+1\right)}=\dfrac{11}{2}-\dfrac{\left(3x+1\right)^2}{2\left(x^2+1\right)}\le\dfrac{11}{2}\)
\(y_{max}=\dfrac{11}{2}\) khi \(x=-\dfrac{1}{3}\)
\(y=\dfrac{2x^2-6x+10}{2\left(x^2+1\right)}=\dfrac{x^2+1+x^2-6x+9}{2\left(x^2+1\right)}=\dfrac{1}{2}+\dfrac{\left(x-3\right)^2}{2\left(x^2+1\right)}\ge\dfrac{1}{2}\)
\(y_{min}=\dfrac{1}{2}\) khi \(x=3\)
KH
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 5 2021
Từ pt (E) ta xác định được: \(a=5;b=3;c=4\)
\(F_1F_2=2c=8\Rightarrow\) chu vi tam giác \(MF_1F_2=MF_1+MF_2+F_1F_2=2a+2c=18\)
\(\Rightarrow\) nửa chu vi \(p=9\)
Tam giác \(MF_1F_2\) vuông tại M \(\Rightarrow OM=\dfrac{1}{2}F_1F_2=4\)
Gọi \(M\left(x;y\right)\Rightarrow\overrightarrow{OM}=\left(x;y\right)\Rightarrow OM^2=x^2+y^2=16\)
\(\Rightarrow x^2=16-y^2\)
Thay vào pt (E):
\(\dfrac{16-y^2}{25}+\dfrac{y^2}{9}=1\Rightarrow y^2=\dfrac{81}{16}\Rightarrow\left|y\right|=\dfrac{9}{4}\)
\(S_{MF_1F_2}=\dfrac{1}{2}F_1F_2.d\left(M;F_1F_2\right)=\dfrac{1}{2}.2c.\left|y\right|=9\)
\(\Rightarrow r=\dfrac{S_{MF_1F_2}}{p}=1\)
HP
20 tháng 5 2021
13.
\(\dfrac{sinx-sin3x+sin5x}{cosx-cos3x+cos5x}\)
\(=\dfrac{2sin3x.cos2x-sin3x}{2cos3x.cos2x-cos3x}\)
\(=\dfrac{\left(2cos2x-1\right)sin3x}{\left(2cos2x-1\right)cos3x}\)
\(=\dfrac{sin3x}{cos3x}=tan3x\)
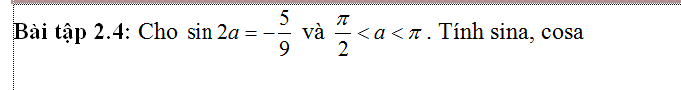
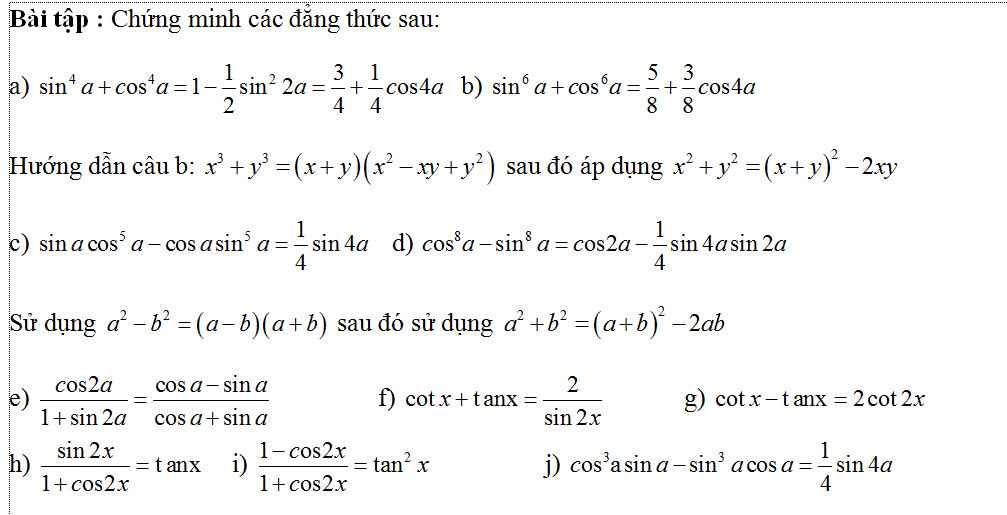
\(\dfrac{\pi}{2}< a< \pi\Rightarrow\left\{{}\begin{matrix}sina>0\\cosa< 0\end{matrix}\right.\)
\(sin2a=-\dfrac{5}{9}\Leftrightarrow sina.cosa=-\dfrac{5}{18}\Rightarrow cosa=-\dfrac{5}{18sina}\)
Thế vào \(sin^2a+cos^2a=1\)
\(sin^2a+\dfrac{25}{324sin^2a}=1\Leftrightarrow sin^4a-sin^2a+\dfrac{25}{324}=0\)
\(\Rightarrow\left[{}\begin{matrix}sin^2a=\dfrac{9-2\sqrt{14}}{8}\\sin^2a=\dfrac{9+2\sqrt{14}}{8}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}sina=\sqrt{\dfrac{9-2\sqrt{14}}{8}};cosa=-\sqrt{\dfrac{9+2\sqrt{14}}{8}}\\sina=\sqrt{\dfrac{9+2\sqrt{14}}{8}};cosa=-\sqrt{\dfrac{9-2\sqrt{14}}{8}}\end{matrix}\right.\)