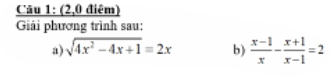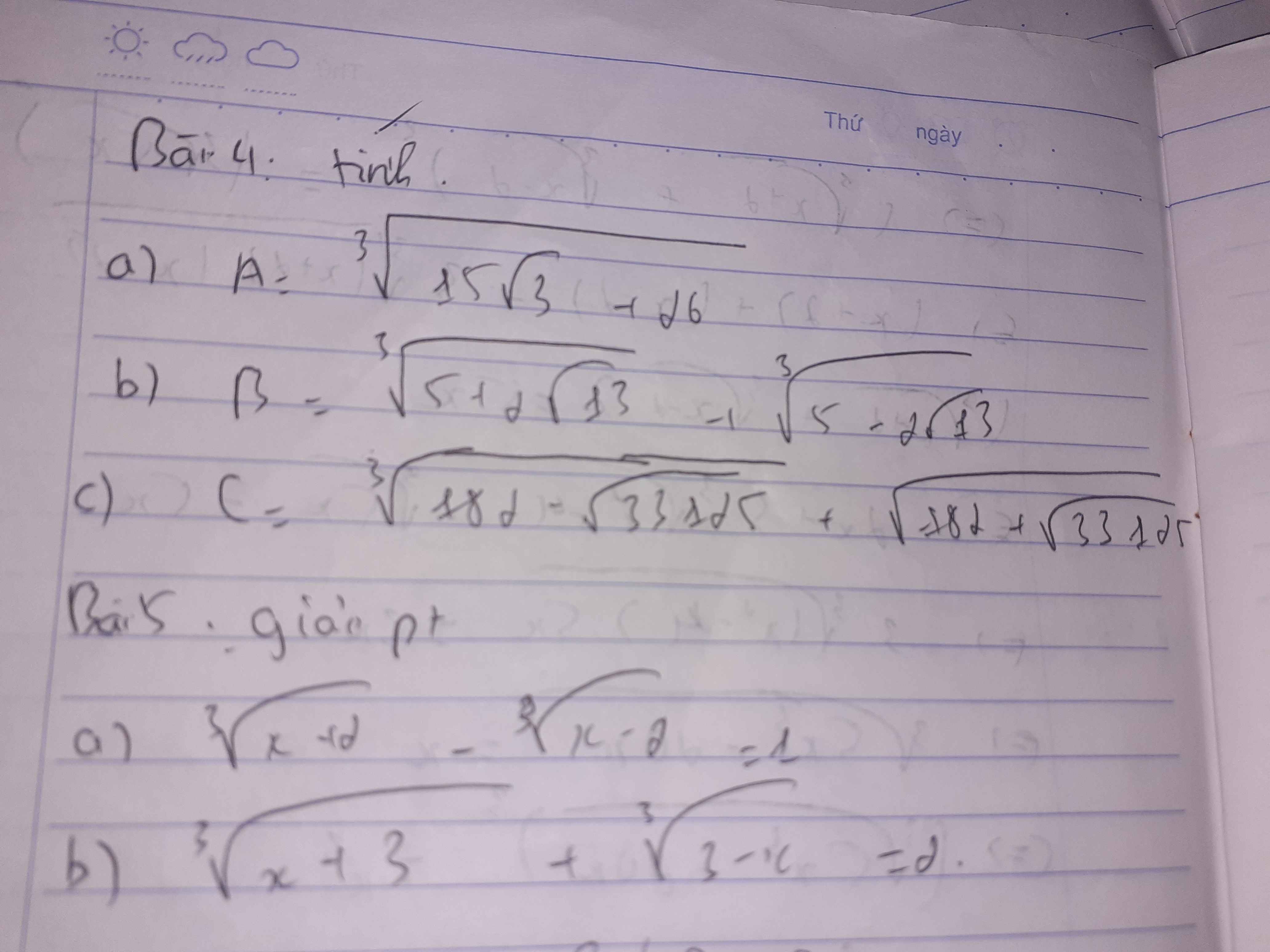K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 12 2021
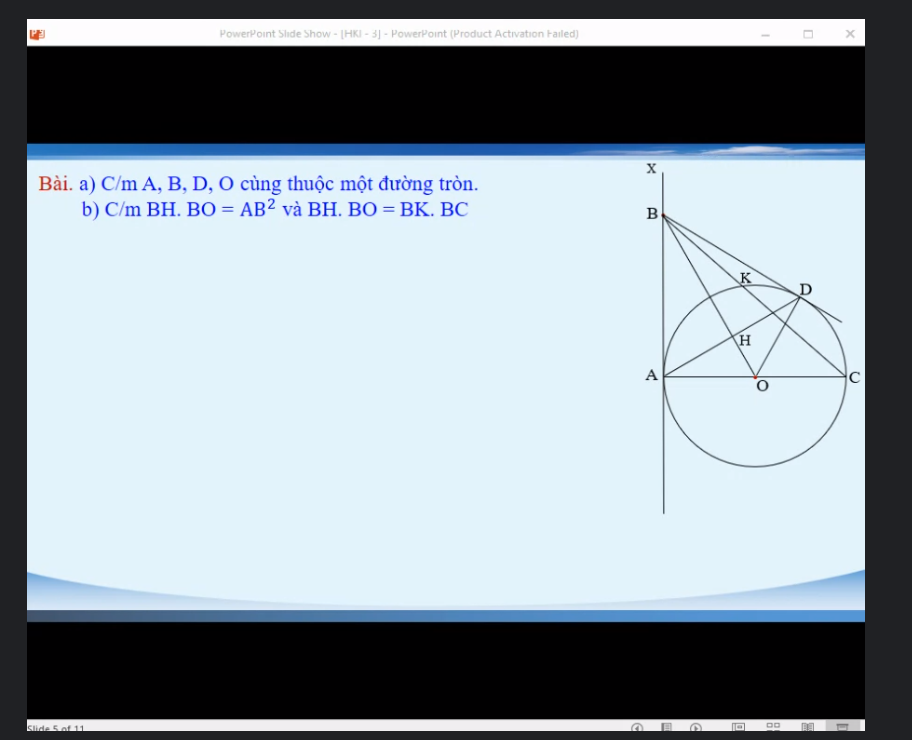
a: Xét tứ giác BAOD có
\(\widehat{BAO}+\widehat{BDO}=180^0\)
Do đó: BAOD là tứ giác nội tiếp
23 tháng 11 2021
\(a,\Leftrightarrow m+1=-2\Leftrightarrow m=-3\\ \text{Vì }-3< 0\text{ nên hàm số nghịch biến}\)
23 tháng 11 2021
\(2,\left(d_1\right)//\left(d_2\right)\Leftrightarrow\left\{{}\begin{matrix}m+1=3m^2+3m\\3\ne5\end{matrix}\right.\Leftrightarrow3m^2+2m-1=0\\ \Leftrightarrow\left[{}\begin{matrix}m=\dfrac{1}{3}\left(l\right)\\m=-1\left(n\right)\end{matrix}\right.\\ \Leftrightarrow m=-1\)
HP
6 tháng 9 2021
4.
a, \(A=\sqrt[3]{15\sqrt{3}+26}=\sqrt[3]{\left(\sqrt{3}+2\right)^3}=\sqrt{3}+2\)
b, \(B=\sqrt[3]{5+2\sqrt{13}}+\sqrt[3]{5-2\sqrt{13}}\)
\(\Rightarrow2B=\sqrt[3]{40+16\sqrt{13}}+\sqrt[3]{40-16\sqrt{13}}\)
\(=\sqrt[3]{\left(\sqrt{13}+1\right)^3}+\sqrt[3]{\left(\sqrt{13}-1\right)^3}\)
\(=\sqrt{13}+1+\sqrt{13}-1=2\sqrt{13}\)
\(\Rightarrow B=\sqrt{13}\)
c, \(C=\sqrt[3]{182-\sqrt{33125}}+\sqrt[3]{182+\sqrt{33125}}\)
\(\Rightarrow C^3=364+3\sqrt[3]{182-\sqrt{33125}}.\sqrt[3]{182+\sqrt{33125}}\left(\sqrt[3]{182-\sqrt{33125}}+\sqrt[3]{182+\sqrt{33125}}\right)\)
\(=364-3C\)
\(\Rightarrow C^3+3C-364=0\)
\(\Leftrightarrow C=7\)
13 tháng 8 2021
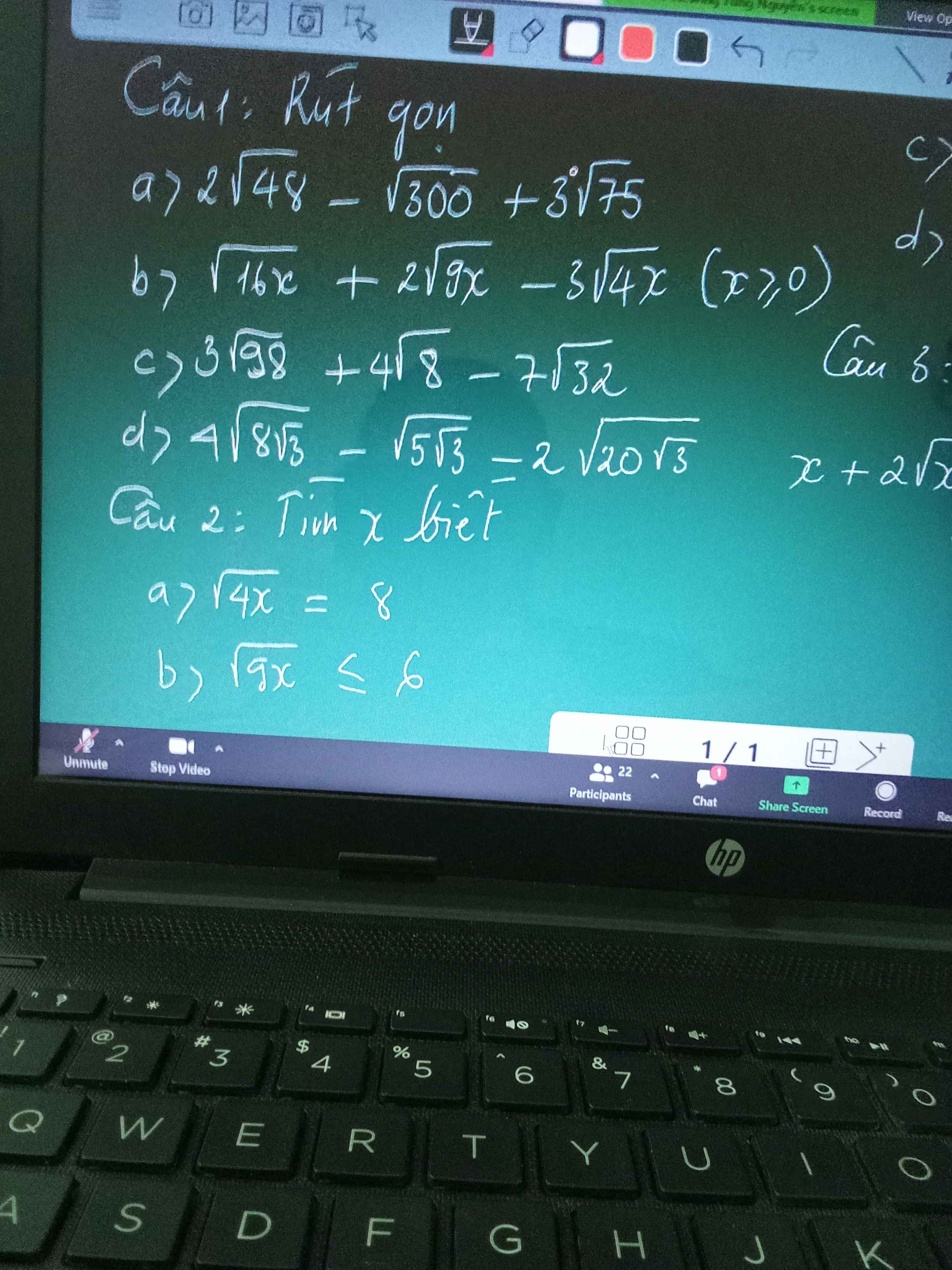
Câu 1
a)=\(8\sqrt{3}-10\sqrt{3}+15\sqrt{3}=13\sqrt{3}\)
b)=\(4\sqrt{x}+6\sqrt{x}-6\sqrt{x}=4\sqrt{x}\)
c)=\(21\sqrt{2}+8\sqrt{2}-28\sqrt{2}=\sqrt{2}\)
d)\(\Rightarrow\)\(8\sqrt{2\sqrt{3}}-\sqrt{5\sqrt{3}}-4\sqrt{5\sqrt{3}}\)
\(\Rightarrow\)\(8\sqrt{2\sqrt{3}}-5\sqrt{5\sqrt{3}}\)
câu 2
a)\(\Rightarrow4x=64\)\(\Rightarrow x=16\)
b)\(\Rightarrow9x\le36\)\(\Rightarrow x\le4\)
13 tháng 8 2021
Câu 2:
a: Ta có: \(\sqrt{4x}=8\)
\(\Leftrightarrow4x=64\)
hay x=16
b: Ta có: \(\sqrt{9x}\le6\)
\(\Leftrightarrow9x\le36\)
\(\Leftrightarrow x\le4\)
Kết hợp ĐKXĐ, ta được: \(0\le x\le4\)
3 tháng 7 2021
a) Ta có: \(P=\dfrac{a\sqrt{a}-1}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}+\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\left(\dfrac{3\sqrt{a}}{\sqrt{a}-1}-\dfrac{\sqrt{a}+2}{\sqrt{a}+1}\right)\)
\(=\dfrac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}+1\right)}+\dfrac{a-1}{\sqrt{a}}\cdot\dfrac{3\sqrt{a}\left(\sqrt{a}+1\right)-\left(\sqrt{a}+2\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=\dfrac{a+\sqrt{a}+1-a+\sqrt{a}-1}{\sqrt{a}}+\dfrac{3a+3\sqrt{a}-\left(a-\sqrt{a}+2\sqrt{a}-2\right)}{\sqrt{a}}\)
\(=2+\dfrac{3a+3\sqrt{a}-a+\sqrt{a}-2\sqrt{a}+2}{\sqrt{a}}\)
\(=\dfrac{2\sqrt{a}+2a+2\sqrt{a}+2}{\sqrt{a}}\)
\(=\dfrac{2\left(a+2\sqrt{a}+1\right)}{\sqrt{a}}\)
\(=\dfrac{2\left(\sqrt{a}+1\right)^2}{\sqrt{a}}\)
b) Ta có: \(P-6=\dfrac{2\left(\sqrt{a}+1\right)^2-6\sqrt{a}}{\sqrt{a}}\)
\(=\dfrac{2a+4\sqrt{a}+2-6\sqrt{a}}{\sqrt{a}}\)
\(=\dfrac{2\left(a-\sqrt{a}+1\right)}{\sqrt{a}}>0\forall a\) thỏa mãn ĐKXĐ
hay P>6
15 tháng 7 2021
Câu 1:
1) Ta có: \(2x^2+5x-3=0\)
\(\Leftrightarrow2x^2+6x-x-3=0\)
\(\Leftrightarrow\left(x+3\right)\left(2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=\dfrac{1}{2}\end{matrix}\right.\)
2) Để hàm số đồng biến trên R thì m-1>0
hay m>1
15 tháng 7 2021
Câu 1:
3) Ta có: P=a+b-2ab
\(=1+\sqrt{2}+1-\sqrt{2}-2\left(1+\sqrt{2}\right)\left(1-\sqrt{2}\right)\)
\(=2-2\cdot\left(-1\right)=4\)
W
1