K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
3
C
19 tháng 10 2018
\(5-3x^2+6x=-3x^2+6x+5=-3\left(x^2-2x-5\right)\)
\(=-3\left(x^2-2x+1-6\right)\)
\(=-3\left(x^2-2x+1\right)+18\)
\(=-3\left(x-1\right)^2+18\le18\forall x\)
Dấu = xảy ra khi: \(-3\left(x-1\right)^2=0\Leftrightarrow x=1\)
Vậy : GTLN là 18 tại x = 1
T
20 tháng 10 2018
Nguyễn Hoàng Khánh Dương sai rồi nha bạn! Bạn thay x = 1 vào biểu thức xem có ra được giá trị MAX = 18 không???
Gọi biểu thức trên là A.Ta có: \(A=5-3x^2+6x=-3x^2+6x+5\)
\(=-3x^2+6x-3+8\)
\(=-3\left(x^2-2x+1\right)+8\)
\(=-3\left(x-1\right)^2+8\le8\) (do \(-3\left(x-1\right)^2\le0\forall x\))
Dấu "=" xảy ra \(\Leftrightarrow-3\left(x-1\right)^2=0\Leftrightarrow x=1\)
Vậy \(A_{max}=8\Leftrightarrow x=1\)
giúp mk vs ạ ai nhanh mk tick nha
19 tháng 4 2022
a. xét tam giác ABC và tam giác BHC có:
góc B = góc C = 90o
góc C chung
=> tam giác ABC ~ tam giác BHC (g.g)
Áp dụng định lí Pytago vào tam giác ABC, ta có:
AB2+BC2=AC2
36 + 64= AC2
AC2= 100
AC= 10 (cm)
vì tam giác ABC ~ tam giác BHC
=> \(\dfrac{AB}{BH}\)= \(\dfrac{AC}{BC}\)
=> BH = \(\dfrac{AB.BC}{AC}\)
=> BH= \(\dfrac{6.8}{10}\)= 4,8 (cm)
19 tháng 4 2022
gọi số học sinh mua vở dự kiến là x
số học sinh mua vở trong quá trình thực hiện là x - 15
Theo đề ta có:
5x + 691= 6(x-15)
5x + 691= 6x - 90
5x - 6x = -90 - 691
-x= -781
x= 781
vậy trường có 781 học sinh.
19 tháng 4 2022
a.\(ĐK:x\ne\pm1;x\ne-\dfrac{1}{2}\)
\(P=\left(\dfrac{x}{x+1}-\dfrac{x+1}{x-1}+\dfrac{7x-3}{x^2-1}\right):\dfrac{4}{2x+1}\)
\(P=\left(\dfrac{x\left(x-1\right)-\left(x+1\right)\left(x+1\right)+7x-3}{\left(x-1\right)\left(x+1\right)}\right):\dfrac{4}{2x+1}\)
\(P=\dfrac{x^2-x-x^2-2x-1+7x-3}{\left(x-1\right)\left(x+1\right)}.\dfrac{2x+1}{4}\)
\(P=\dfrac{\left(4x-4\right)\left(2x+1\right)}{4\left(x-1\right)\left(x+1\right)}\)
\(P=\dfrac{4\left(x-1\right)\left(2x+1\right)}{4\left(x-1\right)\left(x+1\right)}\)
\(P=\dfrac{2x+1}{x+1}\)
b.\(2x^2+x=0\)
\(\Leftrightarrow x\left(2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=-\dfrac{1}{2}\left(ktm\right)\end{matrix}\right.\) ( vì \(x\ne-\dfrac{1}{2}\) )
\(x=0\Leftrightarrow P=\dfrac{2.0+1}{0+1}=\dfrac{1}{1}=1\)
TV
1
10 tháng 5 2023
a: =-5(x^2-3/5x+1/5)
=-5(x^2-2*x*3/10+9/100+11/100)
=-5(x-3/10)^2-11/20<=-11/20
Dấu = xảy ra khi x=3/10
b: =7(x^2-5/7x+3/7)
=7(x^2-2*x*5/14+25/196+59/196)
=7(x-5/14)^2+59/28>=59/28
Dấu = xảy ra khi x=5/14
15 tháng 5 2023
\(=7x-7\sqrt{x}+\sqrt{x}-1=\left(\sqrt{x}-1\right)\left(7\sqrt{x}+1\right)\)
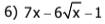
7: Đặt căn x=t(t>=0)
=>2t^2-3t-1=0
=>\(t=\dfrac{3+\sqrt{17}}{4}\)
=>\(x=\dfrac{13+3\sqrt{17}}{8}\)
8: =>(căn x+1)(3 căn x+1)=0
=>\(x\in\varnothing\)