K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 4 2017
Giải:
|
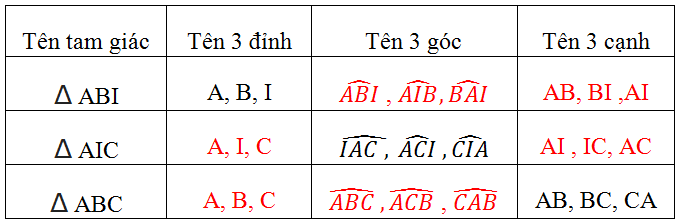
Tên tam giác |
Tên 3 đỉnh |
Tên 3 góc |
Tên 3 cạnh |
|
|
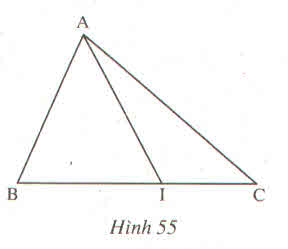
A,B,I |
|
AB, BI, IA |
|
|
A,I,C |
|
AI, IC, CA |
|
|
A,B,C |
|
AB, BC, CA |
18 tháng 4 2017
Giải:
|
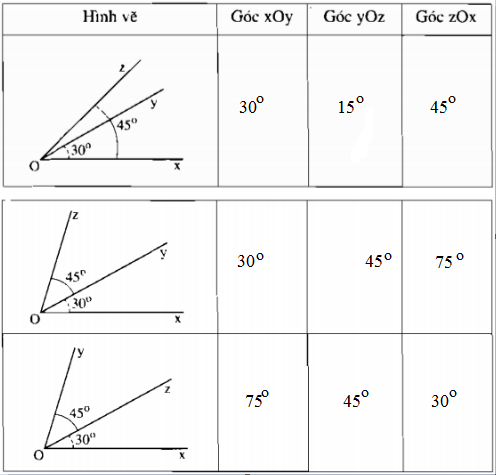
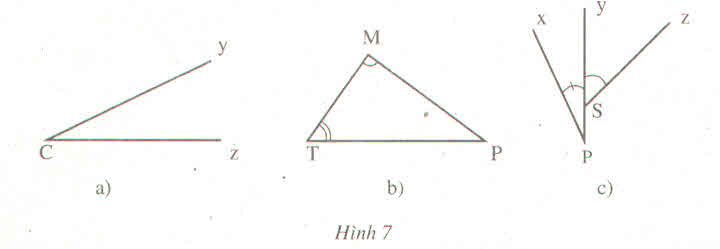
Hình |
Tên góc (cách viết thông thường) |
Tên đỉnh |
Tên cạnh |
Tên góc (Cách viết kí hiệu) |
|
a |
Góc yCz, góc zCy, góc C |
C |
Cy,Cz |
|
|
b |
Góc MTP, PTM, T Góc TMP, PMT,M Góc TPM, MPT,P |
T M P |
TM,TP MT,MP PT,PM |
|
|
c |
Góc xPy,yPx,P Góc ySz,zSy |
P S |
Px, Py Sy, Sz |
|
SG
1
SG
2
SG
4
MP
22 tháng 7 2017
\(\Rightarrow\dfrac{5}{4}-\dfrac{1}{4}x=\dfrac{3}{10}x-\dfrac{2}{5}\)
\(\Rightarrow\dfrac{5}{4}+\dfrac{2}{5}=\dfrac{3}{10}x-\dfrac{1}{4}x\)
\(\Rightarrow\dfrac{33}{20}=\dfrac{11}{20}x\)
\(\Rightarrow x=\dfrac{33}{20}\div\dfrac{11}{20}\)
\(\Rightarrow x=3\)
Q
22 tháng 7 2017
\(1\dfrac{1}{4}-x\dfrac{1}{4}=x\cdot30\%\cdot\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{5}{4}-x\dfrac{1}{4}=x\cdot\dfrac{3}{10}-\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{5}{4}-\dfrac{1}{4}x=\dfrac{3}{10}x-\dfrac{2}{5}\)
\(\Leftrightarrow25-5x=6x-8\)
\(\Leftrightarrow-5x-6x=-8-25\)
\(\Leftrightarrow-11x=-33\)
\(\Leftrightarrow x=3\)
Vậy x = 3
19 tháng 5 2017
Số nguyên biểu thị điểm:
- Điểm N: 2
- Điểm P: -3
- Điểm Q: -5
10 tháng 6 2017
Số nguyên biểu thị điểm:
- Điểm N : 2
- Điểm P : -3
- Điểm Q : -5
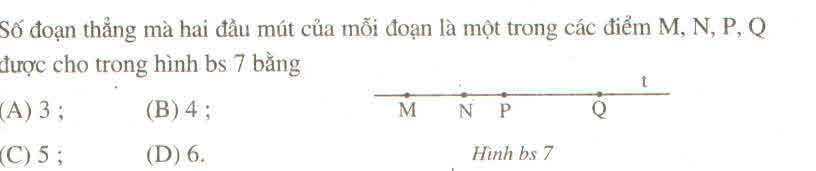
\(A=\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{19.20}=\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{19}-\dfrac{1}{20}=\dfrac{1}{3}-\dfrac{1}{20}< \dfrac{1}{3}\)
\(B=\dfrac{2}{3.4}+\dfrac{2}{4.5}+...+\dfrac{2}{19.20}=2\left(\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{19.20}\right)=2\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{19}-\dfrac{1}{20}\right)=2\left(\dfrac{1}{3}-\dfrac{1}{20}\right)=\dfrac{2}{3}-\dfrac{2}{20}< \dfrac{2}{3}\)
\(C=\dfrac{1}{2.4}+\dfrac{1}{4.6}+...+\dfrac{1}{18.20}=\dfrac{1}{2}\left(\dfrac{2}{2.4}+\dfrac{2}{4.6}+...+\dfrac{2}{18.20}\right)=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{18}-\dfrac{1}{20}\right)=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{20}\right)=\dfrac{1}{4}-\dfrac{1}{40}< \dfrac{1}{4}\)
\(D=\dfrac{1}{4.6}+\dfrac{1}{6.8}+...+\dfrac{1}{18.20}=\dfrac{1}{2}\left(\dfrac{2}{4.6}+\dfrac{2}{6.8}+...+\dfrac{2}{18.20}\right)=\dfrac{1}{2}\left(\dfrac{1}{4}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{8}+...+\dfrac{1}{18}-\dfrac{1}{20}\right)=\dfrac{1}{2}\left(\dfrac{1}{4}-\dfrac{1}{20}\right)=\dfrac{1}{8}-\dfrac{1}{40}< \dfrac{1}{8}\)