Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Có:
\(m=\dfrac{F_{hd}R^2}{GM}=\dfrac{F'_{hd}\left(R+h\right)^2}{GM}\)
\(\Leftrightarrow F_{hd}R^2=F'_{hd}\left(R+h\right)^2\)
\(\Leftrightarrow45R^2=5\left(R^2+h^2+2Rh\right)\)
\(\Leftrightarrow45R^2=5R^2+5h^2+10Rh\)
\(\Leftrightarrow45R^2-5R^2-5h^2-10Rh=0\)
\(\Leftrightarrow40R^2-5h^2-10Rh=0\)
\(\Leftrightarrow h=12800km\)



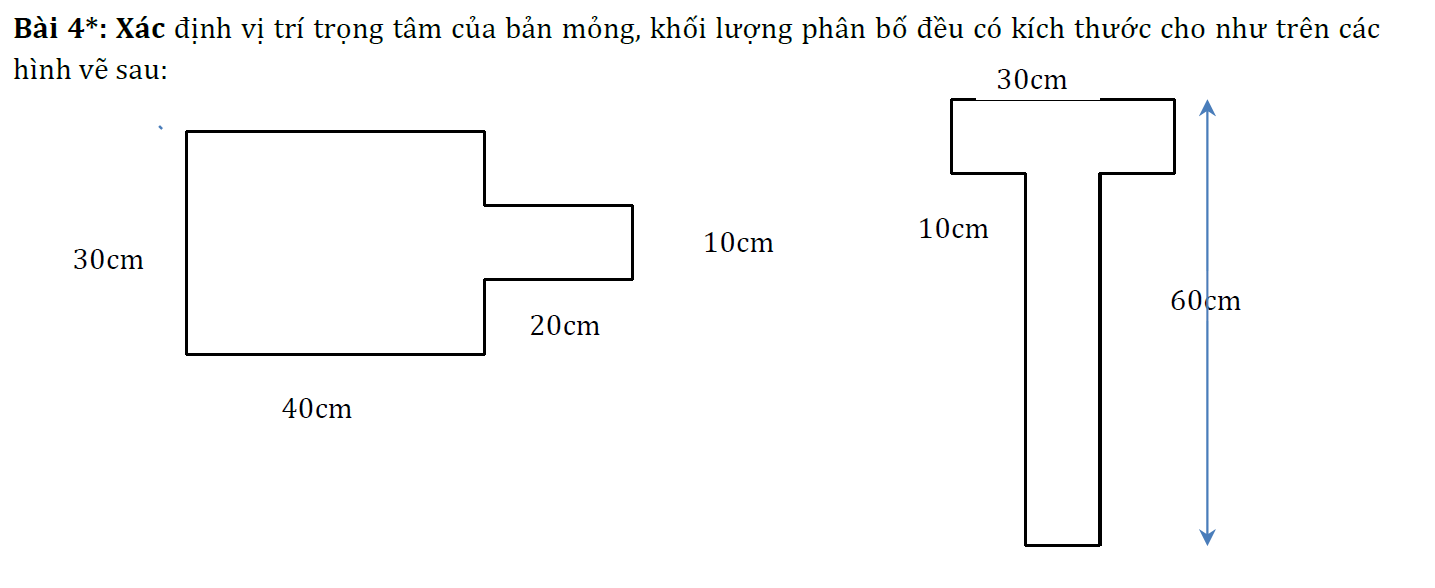
ta có:
\(\dfrac{P_1}{P}=\dfrac{S_1}{S}=\dfrac{\pi R^2}{\dfrac{4}{\pi R^2}}=\dfrac{1}{4}\)
\(\dfrac{P_2}{P}=\dfrac{S-2S_1}{S}=\dfrac{S-\dfrac{S}{2}}{S}=\dfrac{1}{2}\)
<=>\(\dfrac{P_1}{P_2}=\dfrac{1}{\dfrac{4}{\dfrac{1}{2}}}=\dfrac{1}{2}\)
ta tiếp có hệ pt:
\(\left\{{}\begin{matrix}\dfrac{OO_2}{OO_1}=\dfrac{P_1}{P_2}=\dfrac{1}{2}\\OO_2+OO_1=\dfrac{R}{2}\end{matrix}\right.\)
ra được :
\(OO_1=\dfrac{R}{3}\) và \(OO_2=\dfrac{R}{6}\)