
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số tiền thưởng của 3 công nhân lần luotj là x, y, z(đồng)
Ta có:x+y+z=344000
Vì x, y, z TLT(tỉ lệ thuận) với 20; 22; 18 và TLN(tỉ lệ nghịch) với 2; 4; 3
\(\Rightarrow\)x, y, z TLT với 20; 22; 18 và TLT với \(\frac{1}{2};\frac{1}{4};\frac{1}{3}\)tức là x, y, z TLT với \(20\cdot\frac{1}{2};22\cdot\frac{1}{4};18\cdot\frac{1}{3}=10;5,5;6\)
Ta có:\(\frac{x}{10}=\frac{y}{5,5}=\frac{z}{6}\)
và x+y+z=344000
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{10}=\frac{y}{5,5}=\frac{z}{6}\)=\(\frac{x+y+z}{10+5,5+6}=\frac{344000}{21,5}=16000\)
\(\Rightarrow\)x=160000
y=88000
z=96000
Vậy số tiền thưởng của mỗi người lần luotj là 160000;88000;96000

Ta có: \(5xy-3y=2xy-11\)
\(5xy-2xy=-11+3y\)
\(3xy=-11+3y\)
\(3xy-3y=-11\)
\(3y\left(x-1\right)=-11\)
Ta có bảng:
| 3y | 1 | -1 | 11 | -11 |
| y | 1/3 | -1/3 | 11/3 | -11/3 |
| x-1 | -11 | 11 | -1 | 1 |
| x | -10 | 12 | 0 | 2 |

\(\frac{4}{5}\)x \(x\)=\(\frac{8}{35}\)
\(x\)=\(\frac{8}{35}\):\(\frac{4}{5}\)
\(x\)= \(\frac{2}{7}\)


Bài 2:
Lũy thừa với số mũ chẵn của một số hữu tỉ âm là số dương
Lũy thừa với số mũ lẻ của một số hữu tỉ âm là số âm

Bài 13:
a: \(x^3=343\)
nên x=7
b: \(\left(2x-3\right)^2=9\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3\\2x-3=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=0\end{matrix}\right.\)

a: \(A=\dfrac{4^2\cdot4^3}{2^{10}}=\dfrac{4^5}{2^{10}}=1\)
b: \(C=\dfrac{5^4\cdot20^4}{25^5\cdot4^5}=\dfrac{100^4}{100^5}=\dfrac{1}{100}\)

Bài 9:
a: \(10^8\cdot2^8=20^8\)
b: \(10^8:2^8=5^8\)
c: \(25^4\cdot2^8=100^4\)
d: \(27^2:25^3=\left(\dfrac{9}{25}\right)^3\)
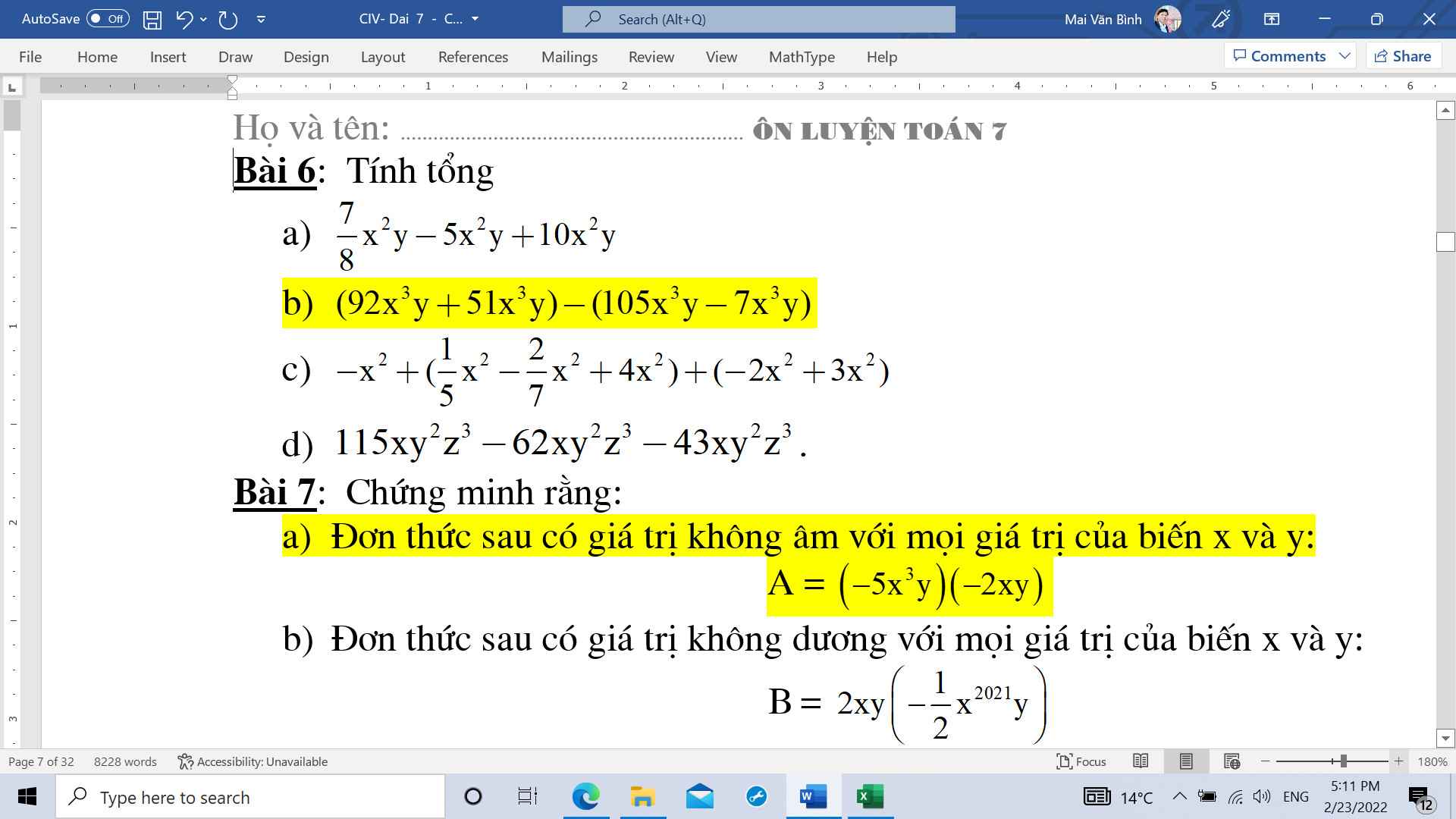
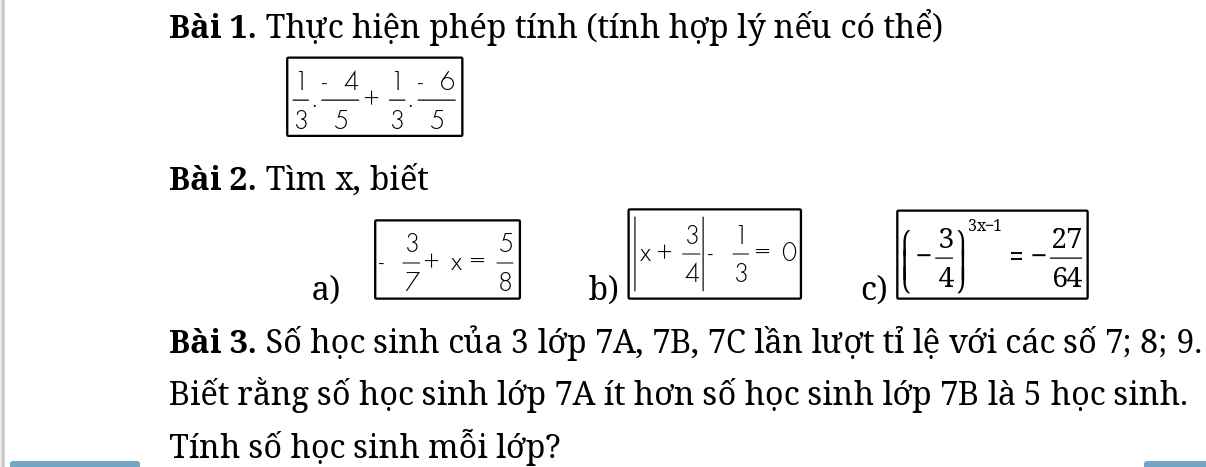 Mọi người ơi , mọi người giúp mình với , mình trân thành cảm ơn
Mọi người ơi , mọi người giúp mình với , mình trân thành cảm ơn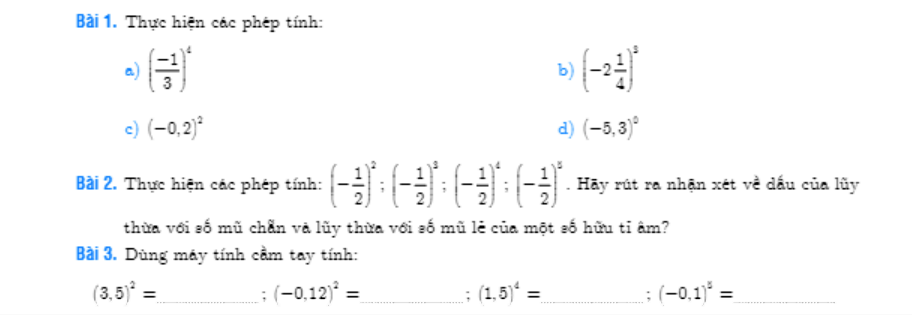


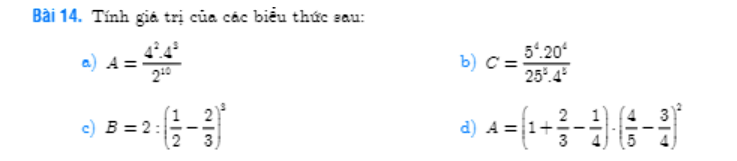

Hộ nè :
\(5\sqrt{16}-4\sqrt{9}+\sqrt{25}-0,3\sqrt{400}\)
\(=5.4-4.3+5-0,3.20\)
\(=20-12+5-6=7\)
có ai ko huhu