
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Giải:
|
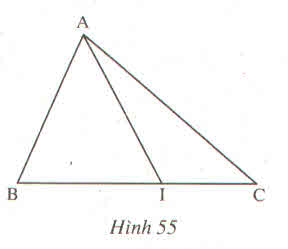
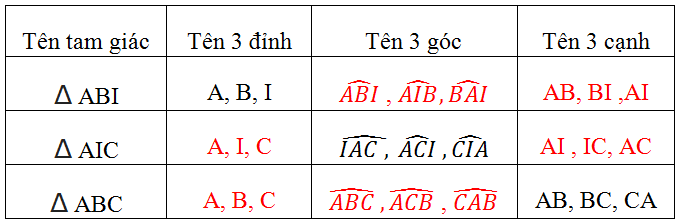
Tên tam giác |
Tên 3 đỉnh |
Tên 3 góc |
Tên 3 cạnh |
|
|
A,B,I |
|
AB, BI, IA |
|
|
A,I,C |
|
AI, IC, CA |
|
|
A,B,C |
|
AB, BC, CA |

Giải:
|
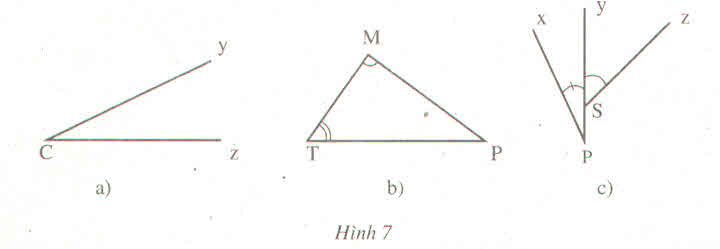
Hình |
Tên góc (cách viết thông thường) |
Tên đỉnh |
Tên cạnh |
Tên góc (Cách viết kí hiệu) |
|
a |
Góc yCz, góc zCy, góc C |
C |
Cy,Cz |
|
|
b |
Góc MTP, PTM, T Góc TMP, PMT,M Góc TPM, MPT,P |
T M P |
TM,TP MT,MP PT,PM |
|
|
c |
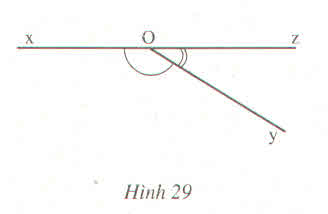
Góc xPy,yPx,P Góc ySz,zSy |
P S |
Px, Py Sy, Sz |
|


Số nguyên biểu thị điểm:
- Điểm N: 2
- Điểm P: -3
- Điểm Q: -5
Số nguyên biểu thị điểm:
- Điểm N : 2
- Điểm P : -3
- Điểm Q : -5

Vẽ đường thẳng x'x . Lấy O bất kì lm gốc chung cho 2 tia đối nhau Ox , Ox' . Lấy 1 độ dài lm đơn vị . Trên mỗi tia , kể từ gốc vẽ liên tiếp các đoạn thẳng có độ dài bằng đơn vị đã chọn . Trên tia Ox , ghi các mốc liên tiếp bằng các số 0,1,2,3,... Số 0 ứng vs điểm O. Trên tia Ox' ghi các mốc liên tiếp bằng số -1 , -2 , -3 , ....













\(\dfrac{5}{2\cdot4}+\dfrac{5}{4\cdot6}+...+\dfrac{5}{48\cdot50}\\ =\dfrac{5}{2}\left(\dfrac{2}{2\cdot4}+\dfrac{2}{4\cdot6}+...+\dfrac{2}{48\cdot50}\right)\\ =\dfrac{5}{2}\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{48}-\dfrac{1}{50}\right)\\ =\dfrac{5}{2}\left(\dfrac{1}{2}-\dfrac{1}{50}\right)=\dfrac{5}{2}\cdot\dfrac{12}{25}=\dfrac{6}{5}\)
Ta có: \(\dfrac{5}{2\cdot4}+\dfrac{5}{4\cdot6}+...+\dfrac{5}{48\cdot50}\)
\(=\dfrac{5}{2}\cdot\left(\dfrac{2}{2\cdot4}+\dfrac{2}{4\cdot6}+...+\dfrac{2}{48\cdot50}\right)\)
\(=\dfrac{5}{2}\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{48}-\dfrac{1}{50}\right)\)
\(=\dfrac{5}{2}\left(\dfrac{1}{2}-\dfrac{1}{50}\right)\)
\(=\dfrac{5}{2}\cdot\dfrac{12}{25}\)
\(=\dfrac{60}{50}=\dfrac{6}{5}\)