Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(d\left(A;\Delta\right)=\dfrac{\left|-3\left(m-2\right)+9\left(m+1\right)-5m+1\right|}{\sqrt{\left(m-2\right)^2+\left(m+1\right)^2}}\)
\(=\dfrac{\left|m+16\right|}{\sqrt{2m^2-2m+5}}=k\Rightarrow\left(m+16\right)^2=k^2\left(2m^2-2m+5\right)\)
\(\Rightarrow\left(2k^2-1\right)m^2-2\left(k^2+16\right)m+5k^2-256=0\)
\(\Delta'=\left(k^2+16\right)^2-\left(2k^2-1\right)\left(5k^2-256\right)\ge0\)
\(\Rightarrow0\le k^2\le61\) \(\Rightarrow k^2_{max}=61\) khi \(m=\dfrac{7}{11}\)

a/ Gọi điểm cố định đó là \(N\left(x_0;y_0\right)\) .
Vì (d) đi qua N nên : \(\left(m-2\right)x_0+\left(m-1\right)y_0-1=0\Leftrightarrow m\left(x_0+y_0\right)-\left(2x_0+y_0+1\right)=0\)
Để (d) luôn đi qua N với mọi m thì \(\begin{cases}x_0+y_0=0\\2x_0+y_0+1=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x_0=-1\\y_0=1\end{cases}\) . Vậy điểm cố định đó là N(-1;1)
b/ Gọi \(A\left(\frac{1}{m-2};0\right)\) và \(B\left(0;\frac{1}{m-1}\right)\) là hai điểm thuộc (d)
và A,B lần lượt nằm trên Ox và Oy
Khi đó \(\frac{1}{h^2}=\frac{1}{OA^2}+\frac{1}{OB^2}\)
hay \(\frac{1}{h^2}=\frac{1}{\left(m-1\right)^2}+\frac{1}{\left(m-2\right)^2}\)
Tới đây bạn tìm GTNN của \(\frac{1}{h^2}\) rồi suy ra GTLN của \(h\) nhé :)

Gọi giao điểm là A, thay tọa độ tham số d1 vào d2:
\(t-2\left(2-t\right)+m=0\Leftrightarrow3t+m-4=0\Rightarrow t=\dfrac{-m+4}{3}\)
\(\Rightarrow A\left(\dfrac{-m+4}{3};\dfrac{m+2}{3}\right)\)
\(\Rightarrow OA=\sqrt{\left(\dfrac{-m+4}{3}\right)^2+\left(\dfrac{m+2}{3}\right)^2}=2\)
\(\Leftrightarrow m^2-2m-8=0\Rightarrow\left[{}\begin{matrix}m=4\\m=-2\end{matrix}\right.\)
b. Bạn không đưa 4 đáp án thì không ai trả lời được câu hỏi này. Có vô số đường thẳng cách đều 2 điểm, chia làm 2 loại: các đường thẳng song song với AB và các đường thẳng đi qua trung điểm của AB
c. Tương tự câu b, do 3 điểm ABC thẳng hàng nên có vô số đường thẳng thỏa mãn, là các đường thẳng song song với AB
b)
A. x-y+2=0
B. x+2y=0
C.2x-2y+10=0
D. x-y+100=0
c)
A. x-3y+4=0
B. -x+y+10=0
C. x+y=0
D. 5x-y+1=0

Khoảng cách AM là nhỏ nhất khi và chỉ khi M là hình chiếu vuông góc của A lên \(\Delta\)
Gọi d là đường thẳng qua A và vuông góc \(\Delta\Rightarrow\) d nhận \(\left(1;-1\right)\) là 1 vtpt
Phương trình d:
\(1\left(x-2\right)-1\left(y-2\right)=0\Leftrightarrow x-y=0\)
M là giao điểm của d và \(\Delta\) nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x+y-2=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\) \(\Rightarrow M\left(1;1\right)\)

Đáp án A
Ta có: ![]()
AM → (3; 2; 4)
Mặt phẳng (P) có vecto pháp tuyến là n p → (1; 1; 1)
Gọi H là hình chiếu vuông góc của A trên d. Ta có: d(A; d) = AH ≤ AM = 29
Dấu bằng xảy ra khi và chỉ khi H trùng M, nghĩa là d vuông góc với AM.
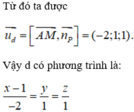
m=11/5