
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Bài 1:
x y m B A C 1 1 2 1
Qua B, vẽ tia Bm sao cho Bm // Ax
Bm // Ax ( cách vẽ ) => góc A1 + góc B1 = 180o ( trong cùng phía )
Mà góc A1 = 140o ( giả thiết ) => góc B1 = 40o
Ta có: góc B1 + góc B2 = góc ABC
Mà góc ABC = 70o ( giả thiết ); góc B1 = 40o ( chứng minh trên )
=> góc B2 = 30o
Ta có: góc B2 + góc C1 = 30o + 150o = 180o
Mà hai góc này ở vị trí trong cùng phía
=> Bm // Cy ( dấu hiệu nhận biết 2 đường thẳng song song )
Ta lại có:
Ax // Bm ( cách vẽ ); Cy // Bm ( chứng minh trên )
=> Ax // Cy ( tính chất 3 quan hệ từ vuông góc đến song song ) ( đpcm )
Bài 3:
A B C F E G N M H 1 2
a) Chứng minh AH < \(\dfrac{1}{2}\) ( AB + AC )
+) Vì AH vuông góc với BC ( giả thiết )
=> AH < AB ( quan hệ giữa đường vuông góc và đường xiên ) ( 1 )
+) Vì AH vuông góc với BC ( giả thiết )
=> AH < AC ( quan hệ giữa đường vuông góc và đường xiên ) ( 2 )
+) Từ ( 1 ) và ( 2 ) => AH + AH < AB + AC
=> 2 . AH < AB + AC
=> AH < \(\dfrac{1}{2}\) ( AB + AC ) ( đpcm )
b) Chứng minh EF = BC
+) Vì BM là đường trung tuyến của tam giác ABC ( giả thiết )
=> \(\dfrac{BG}{BM}=\dfrac{2}{3}\)
=> \(\dfrac{MG}{BG}=\dfrac{1}{2}\)
=> 2 . MG = BG
Mà EM = MG ( do BM là đường trung tuyến của tam giác ABC )
=> EM + MG = BG => EG = BG
+) Vì CN là đường trung tuyến của tam giác ABC ( giả thiết )
=> \(\dfrac{CG}{CN}=\dfrac{2}{3}\)
=> \(\dfrac{GN}{CG}=\dfrac{1}{2}\)
=> 2 . GN = CG
Mà FN = GN ( do CN là đường trung tuyến của tam giác ABC )
=> FN + GN = CG => FG = CG
Góc G1 = góc G2 ( đối đỉnh )
Xét tam giác FEG và tam giác CBG có:
FG = CG ( chứng minh trên )
EG = BG ( chứng minh trên )
Góc G1 = góc G2 ( chứng minh trên )
=> tam giác FEG = tam giác CBG ( c.g.c )
=> EF = BC ( 2 cạnh tương ứng ) ( đpcm )



\(B=\left(\frac{1}{2^2}-1\right).\left(\frac{1}{3^2}-1\right).\left(\frac{1}{4^2}-1\right)......\left(\frac{1}{100^2}-1\right).\)
\(B=\frac{-3}{2^2}\times\frac{-8}{3^2}\times\frac{-15}{4^2}\times.....\times\frac{-9999}{100^2}\)
\(B=-\left(\frac{3}{2^2}\times\frac{8}{3^2}\times.....\times\frac{9999}{100^2}\right)\)(vì A là tích của 99 thừa số âm nên kết quả là âm )
\(B=-\left(\frac{1.3}{2.2}\times\frac{2.4}{3.3}\times.....\times\frac{99.101}{100.100}\right)\)
\(B=-\left(\frac{1.2.3...99}{2.3.4.....100}\times\frac{3.4.5....101}{2.3.4....100}\right)\)
\(B=-\left(\frac{1}{100}\times\frac{101}{2}\right)\)
\(B=-\frac{101}{200}\)

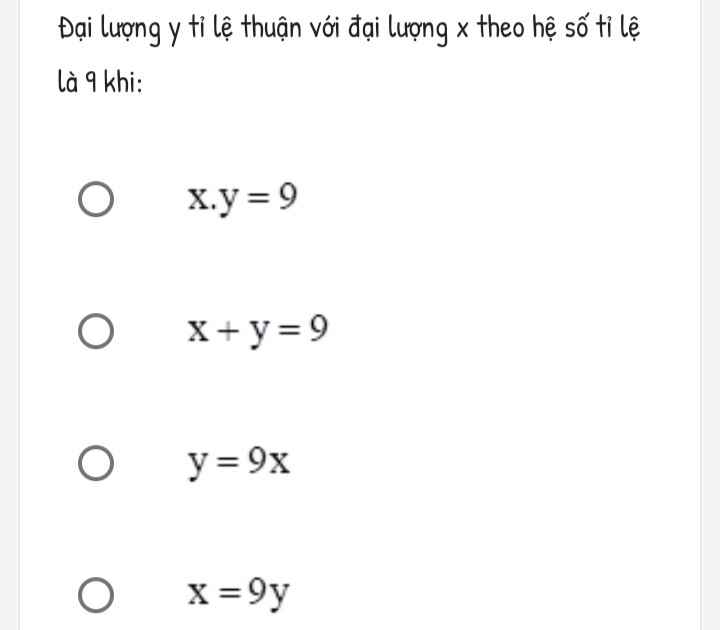






 Giải giúp mình bài 4, 5, 7 với ạ, mình cảm ơn trước ;-;
Giải giúp mình bài 4, 5, 7 với ạ, mình cảm ơn trước ;-; lm giúp mình câu 1b,c với ạ .Mình cảm ơn nhiều!
lm giúp mình câu 1b,c với ạ .Mình cảm ơn nhiều! GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU!!!!
GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU!!!!


Chọn C
C