
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chắc câu c quá, tại tổng 2 ô vuông của hình chữ nhật có 10 chấm tròn. =)
Em nghĩ là câu c vì thấy tổng của các chấm tròn ở mỗi miếng đều là 10.

1.
a. Em tự giải
b.
\(\left\{{}\begin{matrix}2x+y=4m-1\\3x-2y=-m+9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4x+2y=8m-2\\3x-2y=-m+9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7x=7m+7\\y=\dfrac{3x+m-9}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m+1\\y=2m-3\end{matrix}\right.\)
Để \(x+y=7\Rightarrow m+1+2m-3=7\)
\(\Rightarrow3m=9\Rightarrow m=3\)
2.
a. Em tự giải
b.
Phương trình có 2 nghiệm khi:
\(\Delta'=\left(m+1\right)^2-\left(2m+10\right)=m^2-9\ge0\)
\(\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-3\end{matrix}\right.\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=2m+10\end{matrix}\right.\)
Ta có:
\(P=x_1^2+x_2^2+8x_1x_2=\left(x_1+x_2\right)^2+6x_1x_2\)
\(=4\left(m+1\right)^2+6\left(2m+10\right)=4m^2+20m+64\)
\(=4\left(m^2+5m+6\right)+40=4\left(m+2\right)\left(m+3\right)+40\)
Do \(\left[{}\begin{matrix}m\ge3\\m\le-3\end{matrix}\right.\) \(\Rightarrow\left(m+2\right)\left(m+3\right)\ge0\)
\(\Rightarrow P\ge40\)
Vậy \(P_{min}=40\) khi \(m=-3\)
(Nếu bài này giải là \(4m^2+20m+64=\left(2m+5\right)^2+39\ge39\) là sai vì dấu = khi đó xảy ra tại \(m=-\dfrac{5}{2}\) ko thỏa mãn điều kiện \(\Delta\) để pt có nghiệm)

Đáp án b
Các hình màu xanh là phản chiếu của các hình máu cam trong gương.
Nhìn sơ sơ đoán là chọn B
Kiểu 2 hình ở gần (đáy hình cam trên và đỉnh hình xanh dưới sẽ giống nhau), 2 hình còn lại giống nhau tại vị trí đỉnh trên hình cam và đáy dưới hình xanh



đây là bài lớp 10 chứ nhỉ
ta có \(AC=20\times2=40\text{ hải lí}\), \(AB=15\times2=30\text{ hải lí}\)
áp dụng định lý cosin ta có :
\(BC=\sqrt{AB^2+AC^2-2AB.AC\text{c}osA}=\sqrt{40^2+30^2-2\times30\times40\times cos60^o}\simeq36.06\text{ hải lí}\)

b) \(\sqrt{x^2}=\left|-8\right|\)
\(\Rightarrow\left|x\right|=8\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-8\end{matrix}\right.\)
d) \(\sqrt{9x^2}=\left|-12\right|\)
\(\Rightarrow\sqrt{\left(3x\right)^2}=12\)
\(\Rightarrow\left|3x\right|=12\)
\(\Rightarrow\left[{}\begin{matrix}3x=12\\3x=-12\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{12}{3}\\x=-\dfrac{12}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)

ĐKXĐ: \(\left\{{}\begin{matrix}2x-3>=0\\x+1>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\x>=-1\end{matrix}\right.\)
=>\(x>=\dfrac{3}{2}\)
\(\sqrt{2x-3}-\sqrt{x+1}=x-4\)
=>\(\dfrac{2x-3-x-1}{\sqrt{2x-3}+\sqrt{x+1}}-\left(x-4\right)=0\)
=>\(\left(x-4\right)\left(\dfrac{1}{\sqrt{2x-3}+\sqrt{x+1}}-1\right)=0\)
=>x-4=0
=>x=4(nhận)

1.3 Giải phương trình:
a) \(\sqrt{2x+3}=1+\sqrt{2}\)(ĐK: \(x\ge-\frac{3}{2}\))
\(\Leftrightarrow2x+3=\left(1+\sqrt{2}\right)^2=3+2\sqrt{2}\)
\(\Leftrightarrow2x=2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{2}\)(tm)
b) \(\sqrt{x+1}=\sqrt{5}+3\)(ĐK: \(x\ge-1\))
\(\Leftrightarrow x+1=\left(\sqrt{5}+3\right)^2=14+6\sqrt{5}\)
\(\Leftrightarrow x=13+6\sqrt{5}\)(tm)
c) \(\sqrt{3x-2}=2-\sqrt{3}\)(ĐK: \(x\ge\frac{2}{3}\))
\(\Leftrightarrow3x-2=\left(2-\sqrt{3}\right)^2=7-4\sqrt{3}\)
\(\Leftrightarrow x=\frac{9-4\sqrt{3}}{3}\)(tm)
1.4: Phân tích thành nhân tử:
a) \(ab+b\sqrt{a}+\sqrt{a}+1=b\sqrt{a}\left(\sqrt{a}+1\right)+\left(\sqrt{a}+1\right)=\left(b\sqrt{a}+1\right)\left(\sqrt{a}+1\right)\)
b) \(\sqrt{x^3}-\sqrt{y^3}+\sqrt{x^2y}-\sqrt{xy^2}=x\sqrt{x}-y\sqrt{y}+x\sqrt{y}-y\sqrt{x}\)
\(=\left(x-y\right)\left(\sqrt{x}+\sqrt{y}\right)\)
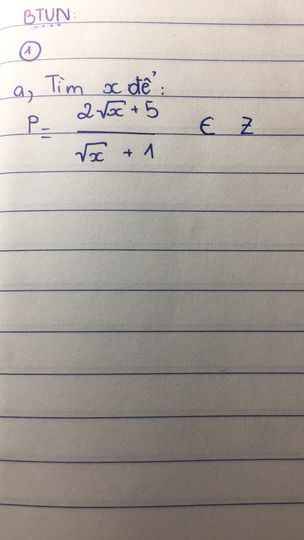

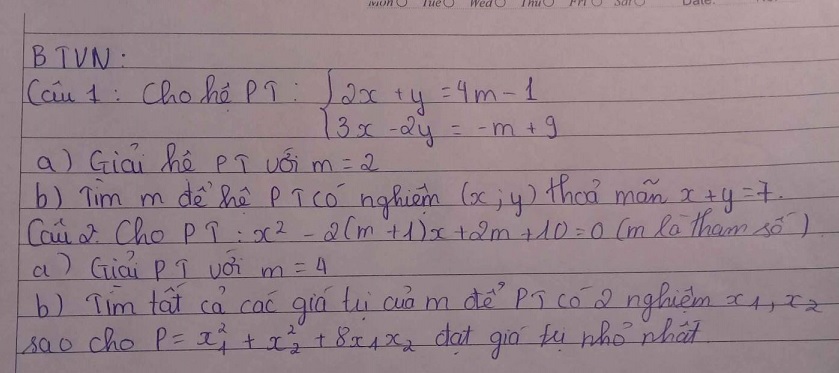


.png)


 Giải giúp mình với ạ, cần gấp lắm, cảm ơn
Giải giúp mình với ạ, cần gấp lắm, cảm ơn

C nguyên
=>2căn x+2+3 chia hết cho căn x+1
=>căn x+1 thuộc Ư(3)
=>căn x+1=1 hoặc căn x+1=3
=>x=4 hoặc x=0
\(P=\dfrac{2\sqrt{x}+5}{\sqrt{x}+1}=\dfrac{2\sqrt{x}+2+3}{\sqrt{x}+1}=2+\dfrac{3}{\sqrt{x}+1}\)`(đk:x >=0)`
Để `P in ZZ`
`=> sqrt(x) +1 in Ư(3)={+-1;+-3}`
Mà `sqrt{x} +1 >0 AA x>=0`
`=> sqrt(x) +1 in {1;3}`
`@ sqrt{x} +1 =1 => x =0`
`@ sqrt(x) +1 =3 => x=4`