
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài làm:
Ta có: \(4x^2-4x-3=0\)
\(\Leftrightarrow\left(4x^2-4x+1\right)-4=0\)
\(\Leftrightarrow\left(2x-1\right)^2-2^2=0\)
\(\Leftrightarrow\left(2x-3\right)\left(2x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x-3=0\\2x+1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{3}{2}\\x=-\frac{1}{2}\end{cases}}\)
Ta có : \(4x^2-4x-3=0\)
\(\Leftrightarrow\left(4x^2-4x+1\right)-4=0\)
\(\Leftrightarrow\left(2x-1\right)^2=4\)
\(\Leftrightarrow\orbr{\begin{cases}2x-1=2\\2x-1=-2\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=\frac{3}{2}\\x=-\frac{1}{2}\end{cases}}\)
Vậy \(x\in\left\{\frac{3}{2};-\frac{1}{2}\right\}\)

`2x - 3 = 5`
`<=> 2x = 5 + 3`
`<=> 2x = 8`
`=> x = 4`
Vậy `S = {4}`
_____________________
`3x - 4 = 11`
`<=> 3x = 11 + 4`
`<=> 3x = 15`
`=> x = 5`
Vậy `S = {5}`
______________
`(2x + 1)(x - 3) = 0`
`<=>` $\left[\begin{matrix} 2x + 1 = 0\\ x - 3 = 0\end{matrix}\right.$
`<=>` $\left[\begin{matrix} x = 1/2\\ x = 3\end{matrix}\right.$
Vậy `S = {1/2; -3}`
__________________
`(2x - 3)(x + 2) = 0`
`<=>` $\left[\begin{matrix} 2x - 3 = 0\\ x + 2 = 0\end{matrix}\right.$
`<=>` $\left[\begin{matrix} x = 3/2\\ x = -2\end{matrix}\right.$
Vậy `S = {-2; 3/2}`

Hình thì bạn tự vẽ nhé !!
Ta có : \(\widehat{CID}=115^o\)
Tổng 2 \(\widehat{ICD}=\widehat{IDC}=65^o\)
Ta tính tổng 2 \(\widehat{C}\)và \(\widehat{D}\)là : \(65^o.2=130^o\)
2 \(\widehat{A}\)và \(\widehat{B}\)là 230o
Ta chỉ thấy có \(\widehat{A}=140^o\)và \(\widehat{B}=90^o\) thì mới phù hợp
Vậy .................


Áp dụng bất đẳng thức về cạnh :
- Trong tam giác OAB : \(AB< OA+OB\left(1\right)\)
- Trong tam giác OCD : \(CD< OC+OD\left(2\right)\)
Cộng (1) và (2) theo vế được : \(AB+CD< OA+OB+OC+OD=AC+BD\)
\(\Rightarrow AB+CD< AC+BD\left(\text{*}\right)\)
Tương tự, ta áp dụng bất đẳng thức về cạnh trong các tam giác ABC , ACD , ABD , BDC được :
- \(\hept{\begin{cases}AC< AB+BC\left(3\right)\\AC< AD+DC\left(4\right)\end{cases}}\)
- \(\hept{\begin{cases}BD< AD+AB\left(5\right)\\BD< CD+BC\left(6\right)\end{cases}}\)
Cộng (3) , (4) , (5) , (6) theo vế được :
\(2\left(AC+BD\right)< 2\left(AB+BC+CD+AD\right)\Rightarrow AC+BD< AB+BC+CD+AD\left(\text{*}\text{*}\right)\)
Từ (*) và (**) ta được điều phải chứng minh.
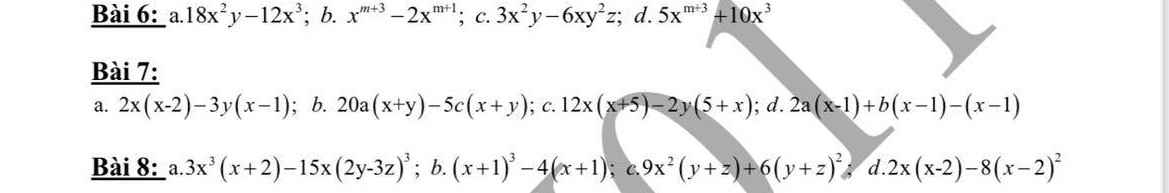 giúp mình nhanh với mình sắp học rồi.Camon các bạn rất nhìu :>>
giúp mình nhanh với mình sắp học rồi.Camon các bạn rất nhìu :>>
