
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


8.
Hàm có 1 điểm cực đại \(\left(x=-1\right)\)
9.
Hàm có 1 điểm cực tiểu (\(x=-1\))
14.
\(y'=\dfrac{2x\left(x+1\right)-\left(x^2+3\right)}{\left(x+1\right)^2}=\dfrac{x^2+2x-3}{\left(x+1\right)^2}\)
\(y'=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
Xét dấu y' trên trục số:
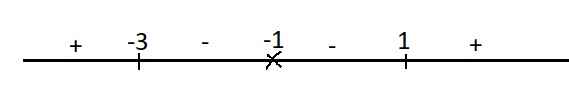
Từ dấu của y' ta thấy \(x=1\) là điểm cực tiểu
\(\Rightarrow y_{CT}=y\left(1\right)=2\)

1.
\(y'=6x^2+6\left(m-1\right)x+6\left(m-2\right)=6\left(x+1\right)\left(x+m-2\right)\)
\(y'=0\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-m+2\end{matrix}\right.\)
Phương trình nghịch biến trên đoạn có độ dài lớn hơn 3 khi:
\(\left|-1-\left(-m+2\right)\right|>3\)
\(\Leftrightarrow\left|m-3\right|>3\Rightarrow\left[{}\begin{matrix}m>6\\m< 0\end{matrix}\right.\)
2.
\(y'=-3x^2+6x+m-1\)
\(\Delta'=9+3\left(m-1\right)>0\Rightarrow m>-2\)
Gọi \(x_1;x_2\) là 1 nghiệm của pt \(-3x^2+6x+m-1=0\Rightarrow\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=\dfrac{-m+1}{3}\end{matrix}\right.\)
Hàm đồng biến trên đoạn có độ dài lớn hơn 1 khi:
\(\left|x_1-x_2\right|>1\)
\(\Leftrightarrow\left(x_1-x_2\right)^2>1\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2>1\)
\(\Leftrightarrow4-\dfrac{-4m+4}{3}>1\)
\(\Rightarrow m>-\dfrac{5}{4}\) \(\Rightarrow m=-1\)
Có đúng 1 giá trị nguyên âm của m thỏa mãn
3.
\(y'=x^2+6\left(m-1\right)x+9\)
\(\Delta'=9\left(m-1\right)^2-9>0\Rightarrow\left[{}\begin{matrix}m>1\\m< 0\end{matrix}\right.\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-6\left(m-1\right)\\x_1x_2=9\end{matrix}\right.\)
\(\left|x_1-x_2\right|=6\sqrt{3}\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=108\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=108\)
\(\Leftrightarrow36\left(m-1\right)^2-36=108\)
\(\Rightarrow\left(m-1\right)^2=4\Rightarrow\left[{}\begin{matrix}m=3\\m=-1\end{matrix}\right.\)
Có 1 giá trị nguyên âm của m thỏa mãn

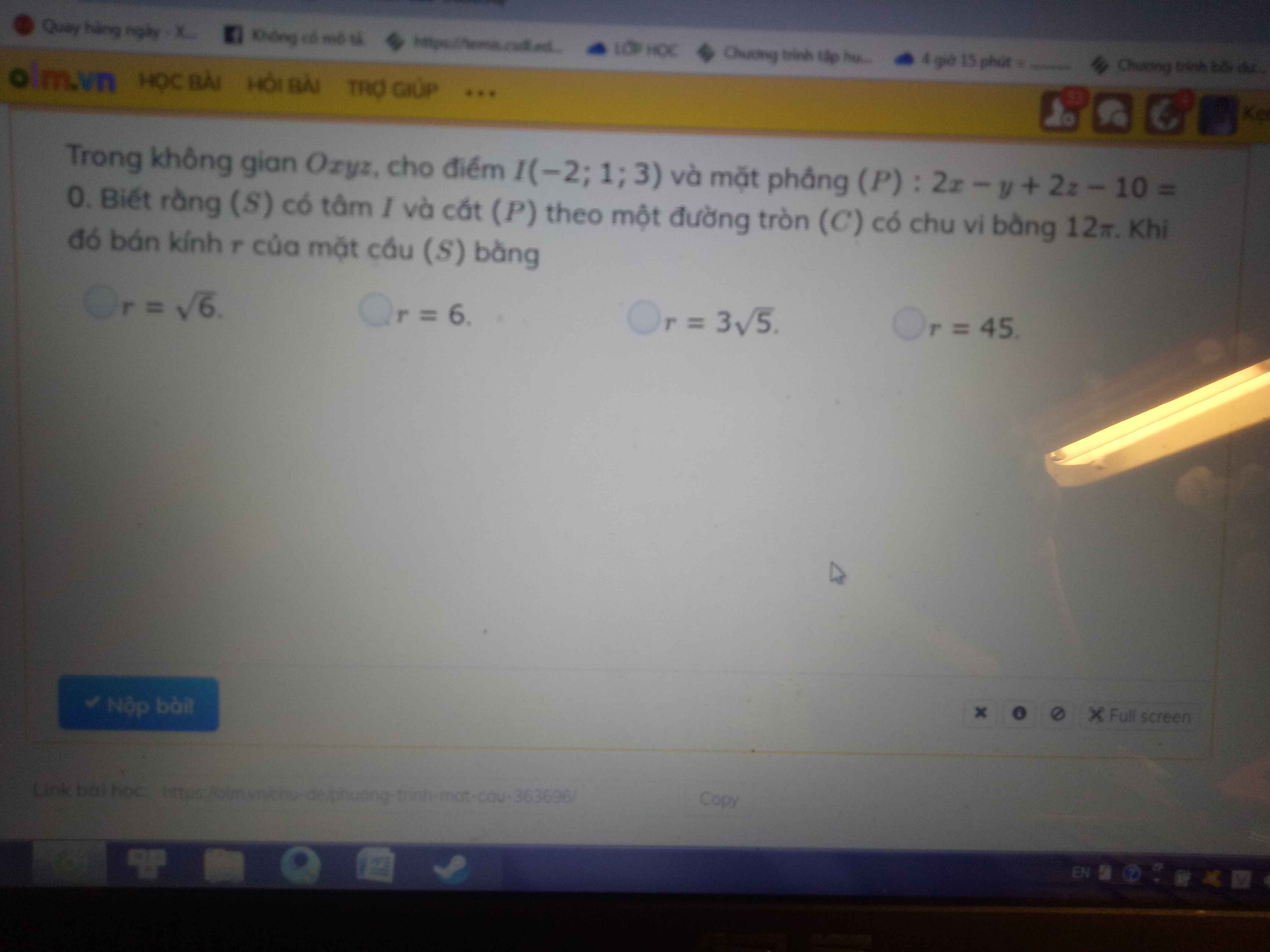
Gọi R là bán kính (C) \(\Rightarrow2\pi R=12\pi\Rightarrow R=6\)
Gọi \(J\) là tâm (C) \(\Rightarrow IJ\perp\left(P\right)\Rightarrow IJ=d\left(I;\left(P\right)\right)\)
\(d\left(I;\left(P\right)\right)=\dfrac{\left|2.\left(-2\right)-1.1+2.3-10\right|}{\sqrt{2^2+\left(-1\right)^2+2^2}}=3\)
\(\Rightarrow IJ=3\)
Áp dụng định lý Pitago:
\(r^2=IJ^2+R^2=45\Rightarrow r=3\sqrt{5}\)
Đường tròn (C)(C) có bán kính R = 6R=6.
d(I,(P))=3.
Mặt cầu (S) cắt mặt phẳng (P) theo một đường tròn
(C)(C) nên có bán kính:
r=\(\sqrt{R^2+(d(I,(P)))^2 } =3\sqrt{5}
\)(P(P) theo một đường tròn (C)(C) nên có bán kính:(S)(S) cắt mặt phẳng (P)

\(\left(1-\dfrac{1}{2}\right)\):\(\left(1-\dfrac{1}{3}\right)\):\(\left(1-\dfrac{1}{4}\right)\):\(\left(1-\dfrac{1}{5}\right)\):\(\left(1-\dfrac{1}{6}\right)\):\(\left(1-\dfrac{1}{7}\right)\)
=\(\left(\dfrac{2-1}{2}\right)\):\(\left(\dfrac{3-1}{3}\right)\):\(\left(\dfrac{4-1}{4}\right)\):\(\left(\dfrac{5-1}{5}\right)\):\(\left(\dfrac{6-1}{6}\right)\)
=\(\dfrac{1}{2}\):\(\dfrac{2}{3}\):\(\dfrac{3}{4}\):\(\dfrac{4}{5}\):\(\dfrac{5}{6}\)
=\(\dfrac{1.\left(3.4.5\right)6}{\left(3.4.5\right)\left(2.2\right)}\)
=\(\dfrac{6}{2.2}=\dfrac{3}{2}\)


31.
\(y'=\dfrac{1+m}{\left(x+1\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi:
\(\dfrac{1+m}{\left(x+1\right)^2}>0\Rightarrow m>-1\) (C)
32.
\(y'=\dfrac{4-m^2}{\left(x+4\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi:
\(4-m^2>0\Rightarrow-2< m< 2\)
\(\Rightarrow m=\left\{-1;0;1\right\}\)
Có 3 giá trị nguyên của m
33.
\(y'=\dfrac{m-1}{\left(x+1\right)^2}\)
Hàm đồng biến trên từng khoảng xác định khi:
\(m-1>0\Rightarrow m>1\)
34.
\(y'=\dfrac{2m-1}{\left(x+2m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}2m-1>0\\-2m>-3\end{matrix}\right.\) \(\Rightarrow\dfrac{1}{2}< m< \dfrac{3}{2}\)
\(\Rightarrow m=1\)
Có 1 giá trị nguyên của m


Em chỉ cần chú ý là bán \(\dfrac{1}{2}\) số còn lại mà đang còn dư 18 lít thì số còn lại sau khi bán một nửa là 36 lít. Từ đó suy ra cả thùng chưa bán có tất cả 72 lít





 mọi người giúp mình với
mọi người giúp mình với

\(y'=-3x^2+3=0\Rightarrow x=\pm1\)
\(y\left(-1\right)=3\) ; \(y\left(1\right)=7\) ; \(y\left(0\right)=5\) ; \(y\left(2\right)=3\)
\(\Rightarrow\min\limits_{\left[0;2\right]}y=3\)